
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 与椭圆的左、右顶点连线的斜率之积为
与椭圆的左、右顶点连线的斜率之积为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 上存在两点
上存在两点![]() ,使得
,使得![]() 的垂心(三角形三条高的交点)恰为坐标原点
的垂心(三角形三条高的交点)恰为坐标原点![]() ,试求直线
,试求直线![]() 的方程.
的方程.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,设O为AC1与A1C的交点,点P为BC的中点.求证:
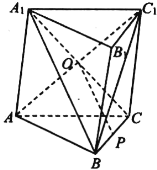
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
科目:高中数学 来源: 题型:
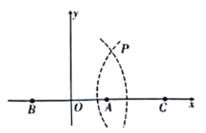
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 台发射的电磁波比
台发射的电磁波比![]() 台电磁波早
台电磁波早![]() (已知电磁波在空气中的传播速度约为
(已知电磁波在空气中的传播速度约为![]() ,1海里
,1海里![]() ),则点
),则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区在一次考试后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩(x)和物理成绩(y),绘制成如图散点图:
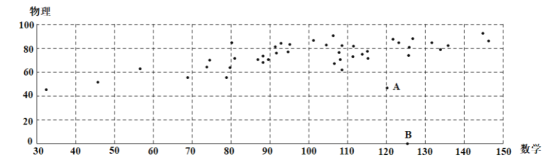
根据散点图可以看出y与x之间有线性相关关系,但图中有两个异常点A,B.经调查得知,A考生由于重感冒导致物理考试发挥失常,B考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
其中xi,yi分别表示这42名同学的数学成绩、物理成绩,i=1,2,…,42,y与x的相关系数r=0.82.
(1)若不剔除A,B两名考生的数据,用44组数据作回归分析,设此时y与x的相关系数为r0.试判断r0与r的大小关系,并说明理由;
(2)求y关于x的线性回归方程(系数精确到0.01),并估计如果B考生加了这次物理考试(已知B考生的数学成绩为125分),物理成绩是多少?(精确到个位);
(3)从概率统计规律看,本次考试该地区的物理成绩ξ服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
作为μ的估计值,用样本方差s2作为σ2的估计值.试求该地区5000名考生中,物理成绩位于区间(62.8,85.2)的人数Z的数学期望.
附:①回归方程![]() 中:
中: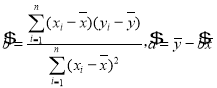
②若![]() ,则
,则![]()
③![]() 11.2
11.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂预购软件服务,有如下两种方案:
方案一:软件服务公司每日收取工厂60元,对于提供的软件服务每次10元;
方案二:软件服务公司每日收取工厂200元,若每日软件服务不超过15次,不另外收费,若超过15次,超过部分的软件服务每次收费标准为20元.
(1)设日收费为![]() 元,每天软件服务的次数为
元,每天软件服务的次数为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)该工厂对过去100天的软件服务的次数进行了统计,得到如图所示的条形图,依据该统计数据,把频率视为概率,从节约成本的角度考虑,从两个方案中选择一个,哪个方案更合适?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种质地均匀的正四面体玩具的4个面上分别标有数字0,1,2,3,将这个玩具抛掷![]() 次,记第
次,记第![]() 次抛掷后玩具与桌面接触的面上所标的数字为
次抛掷后玩具与桌面接触的面上所标的数字为![]() ,数列
,数列![]() 的前
的前![]() 和为
和为![]() .记
.记![]() 是3的倍数的概率为
是3的倍数的概率为![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为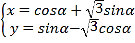 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 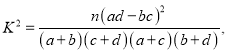
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com