
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 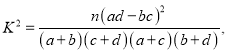
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,已知点![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
: ![]() 上的一点,斜率为
上的一点,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.

(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.
(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面
半径;
(2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动,规则是每邀请一位好友在该平台注册,并购买至少1万元的12月定期,邀请人可获得现金及红包奖励,现金奖励为被邀请人理财金额的![]() ,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
理财金额 |
|
|
|
乙理财相应金额的概率 |
|
|
|
丙理财相应金额的概率 |
|
|
|
(1)求乙、丙理财金额之和不少于5万元的概率;
(2)若甲获得奖励为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.
(1)求证:BE1⊥DC;
(2)求证:DM∥平面BCE1;
(3)判断直线CD与ME1的位置关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com