
【题目】某互联网理财平台为增加平台活跃度决定举行邀请好友拿奖励活动,规则是每邀请一位好友在该平台注册,并购买至少1万元的12月定期,邀请人可获得现金及红包奖励,现金奖励为被邀请人理财金额的![]() ,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
,且每邀请一位最高现金奖励为300元,红包奖励为每邀请一位奖励50元.假设甲邀请到乙、丙两人,且乙、丙两人同意在该平台注册,并进行理财,乙、丙两人分别购买1万元、2万元、3万元的12月定期的概率如下表:
理财金额 |
|
|
|
乙理财相应金额的概率 |
|
|
|
丙理财相应金额的概率 |
|
|
|
(1)求乙、丙理财金额之和不少于5万元的概率;
(2)若甲获得奖励为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据互斥事件的概率公式以及独立事件同时发生的概率公式,可以计算乙、丙理财金额之和不少于5万元的概率值;(2)根据题意, ![]() 的所有可能取值
的所有可能取值![]() ,互斥事件的概率公式以及独立事件同时发生的概率公式计算对应的概率值,写出随机变量
,互斥事件的概率公式以及独立事件同时发生的概率公式计算对应的概率值,写出随机变量![]() 的分布列,计算数学期望值.
的分布列,计算数学期望值.
试题解析:(1)设乙、丙理财金额分别为ξ万元、η万元,则乙、丙理财金额之和不少于5万元的概率为P(ξ+η≥5)=P![]() P
P![]() +P
+P![]() P
P![]() +P
+P![]() P
P![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
(2)X的所有可能的取值为300,400,500,600,700.
P![]() =P
=P![]() P
P![]() =
=![]() ×
×![]() =
=![]() ,
,
P![]() =P
=P![]() P
P![]() +P(ξ=2)P(η=1)=
+P(ξ=2)P(η=1)=![]() ×
×![]() +
+![]() =
=![]() .
.
P![]() =P
=P![]() P
P![]() +P(ξ=3)·P(η=1)+P
+P(ξ=3)·P(η=1)+P![]() P
P![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() =
=![]() ,
,
P![]() =P
=P![]() P
P![]() +P(ξ=3)P(η=2)=
+P(ξ=3)P(η=2)=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() ,
,
P![]() =P(ξ=3)P(η=3) =×=
=P(ξ=3)P(η=3) =×=![]() ×
×![]() =
=![]() .
.
所以X的分布列为
X | 300 | 400 | 500 | 600 | 700 |
P |
|
|
|
|
|
E(X)=300×![]() +400×
+400×![]() +500×
+500×![]() +600×
+600×![]() +700×
+700×![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
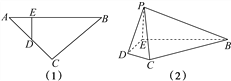
【题目】如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).
(1)求证:PB⊥DE;
(2)若PE⊥BE,PE=1,求点B到平面PEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 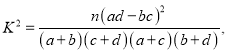
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[-1,1]上的奇函数,在[0,1]上f(x)=2x+ln(x+1)-1.
(1)求函数f(x)的解析式;并判断f(x)在[-1,1]上的单调性(不要求证明);
(2)解不等式f(2x-1)+f(1-x2)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (其中e是自然对数的底数,常数a>0).
(其中e是自然对数的底数,常数a>0).
(1)当a=1时,求曲线在(0,f(0))处的切线方程;
(2)若存在实数x∈(a,2],使得不等式f(x)≤e2成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com