
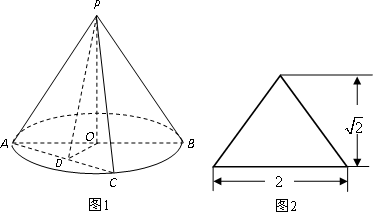
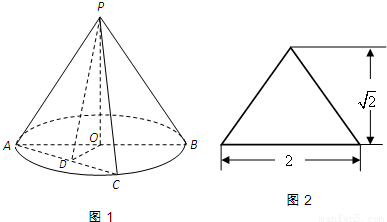
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点.
(Ⅰ) 求该圆锥的侧面积S;
(Ⅱ) 求证:平面PAC⊥平面POD;
(Ⅲ) 若∠CAB=60°,求三棱锥A﹣PBC的体积.

考点:
平面与平面垂直的判定;棱柱、棱锥、棱台的侧面积和表面积;棱柱、棱锥、棱台的体积.
专题:
综合题;空间位置关系与距离.
分析:
(Ⅰ)确定圆的半径,求出圆锥的母线长,可得圆锥的侧面积S;
(Ⅱ) 连接OC,先根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PO⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD⊥平面PAC;
(Ⅲ) 若∠CAB=60°利用等体积转化,可求三棱锥A﹣PBC的体积.
解答:
(Ⅰ)解:由正(主)视图可知圆锥的高![]() ,圆O的直径为AB=2,故半径r=1.
,圆O的直径为AB=2,故半径r=1.
∴圆锥的母线长![]() ,
,
∴圆锥的侧面积![]() . …(4分)
. …(4分)
(Ⅱ)证明:连接OC,
∵OA=OC,D为AC的中点,∴OD⊥AC.
∵PO⊥圆O,AC⊂圆O,∴PO⊥AC.
∵OD∩PO=O,∴AC⊥平面POD.
又AC⊂平面PAC,∴平面PAC⊥平面POD…(8分)
(Ⅲ)解:∵AB是直径,∴∠ACB=90°,又∠CAB=60°,∴![]()
∵PO=![]()
∴三棱锥A﹣PBC的体积为![]() =
=![]() …(12分)
…(12分)
点评:
本题考查三视图,考查面面垂直,考查侧面积与体积,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点.
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点.查看答案和解析>>
科目:高中数学 来源:广东省2012届高三高考压轴卷数学文科试题 题型:044
圆锥PO如图所示,图6是它的正(主)视图.已知圆O的直径为AB,C是![]() 的中点,D为AC的中点.
的中点,D为AC的中点.
(1)求该圆锥的侧面积;
(2)证明:AC⊥平面POD;
(3)求点O到平面PAC的距离.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山西太原五中高二第一学期10月月考理科数学试卷(解析版) 题型:解答题
如图所示,在圆锥PO中, PO=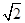 ,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.

(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌二中高三(上)第四次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com