
分析 由题意画出图形,在焦点三角形中由椭圆定义及余弦定理求得|PF1||PF2|的值,代入三角形面积公式得答案.
解答 解:如图,
由椭圆$\frac{{y}^{2}}{12}+\frac{{x}^{2}}{8}=1$,得a2=12,b2=8,c2=4,
∴a=$2\sqrt{3}$,c=2,
在△F1PF2中,由余弦定理得$4{c}^{2}=|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|cos60°$,
即$4{c}^{2}=(|P{F}_{1}|+|P{F}_{2}|)^{2}-3|P{F}_{1}||P{F}_{2}|$,
∴4c2=4a2-3|PF1||PF2|,得|PF1||PF2|=$\frac{32}{3}$.
∴△PF1F2的面积S=$\frac{1}{2}|P{F}_{1}||P{F}_{2}|sin60°=\frac{1}{2}×\frac{32}{3}×\frac{\sqrt{3}}{2}=\frac{8\sqrt{3}}{3}$.
故答案为:$\frac{8\sqrt{3}}{3}$.
点评 本题考查椭圆的简单性质,训练了涉及焦点三角形问题的解法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2) | C. | [-6,+∞) | D. | [-6,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{3}π+kπ,0)$ | B. | $(\frac{2}{3}π+2kπ,0)$ | C. | $(\frac{2}{3}+2k,0)$ | D. | $(\frac{2}{3}+k,0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{2}$) | B. | (-1,1) | C. | (-2,$\frac{1}{2}$) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 服用药 | 10 | 45 | 55 |
| 未服用药 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| P (k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 1.323 | 2.706 | 3.841 | 5.024 | 6.635 | 16.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
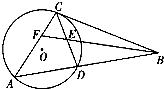 如图,D是△ABC边AB上的一点,△ACD内接于圆O,且∠CAD=∠BCD,E是CD的中点,BE的延长线交AC于点F,证明:
如图,D是△ABC边AB上的一点,△ACD内接于圆O,且∠CAD=∠BCD,E是CD的中点,BE的延长线交AC于点F,证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com