
已知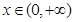 有下列各式:
有下列各式: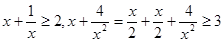 ,
,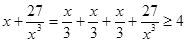 成立,观察上面各式,按此规律若
成立,观察上面各式,按此规律若 ,则正数
,则正数 ( )
( )
| A.4 | B.5 | C.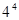 | D.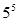 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
由“正三角形的内切圆切于三边的中点”可类比猜想:正四面体的内切球切于四个面( )
| A.各正三角形内一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题“设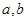 为实数,则方程
为实数,则方程 至少有一个实根”时,要做的假设是( )
至少有一个实根”时,要做的假设是( )
A.方程 没有实根 没有实根 | B.方程 至多有一个实根 至多有一个实根 |
C.方程 至多有两个实根 至多有两个实根 | D.方程 恰好有两个实根 恰好有两个实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆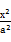 + +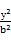 =1的面积S=πab =1的面积S=πab |
| D.以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,那么( )
| A.△A1B1C1和△A2B2C2都是锐角三角形 |
| B.△A1B1C1和△A2B2C2都是钝角三角形 |
| C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形 |
| D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某个命题与正整数有关,如果当n=k(k∈N+)时,该命题成立,那么可
推得当n=k+1时命题也成立.现在已知当n=5时,该命题不成立,那么可推得( ).
| A.当n=6时该命题不成立 |
| B.当n=6时该命题成立 |
| C.当n=4时该命题不成立 |
| D.当n=4时该命题成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com