Question

22.已知常数a>0，在矩形ABCD中，AB＝4，BC＝4a，O为AB的中点.点E、F、G分别在BC、CD、DA上移动，且，P为GE与OF的交点（如图）.问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由.

Answer 1

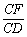
22.解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到两定点距离的和为定值.

　按题意有A（－2，0），B（2，0），C（2，4a），D（－2，4a）.

　设===k（0≤k≤1）.

　由此有E（2，4ak），F（2－4k，4a），G（－2，4a－4ak）.

　直线OF的方程为：2ax+（2k－1）y=0，                                                                          ①

　直线GE的方程为：－a（2k－1）x+y－2a=0.                                                                    ②

　从①，②消去参数k，得点P（x，y）坐标满足方程2a²x²+y²－2ay=0，

　整理得       .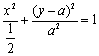

　当a²=时，点P的轨迹为圆弧，所以不存在符合题意的两点.

　当a²≠时，点P轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长.

　

当a²＜时，点P到椭圆两个焦点（－），（）的距离之和为定值.

　

当a²＞时，点P到椭圆两个焦点（0，a－），（0，a+）的距离之和为定值2a.