(Ⅰ)解:因为点
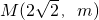
在抛物线C:x
2=ay(a>0)上,所以am=8.
因为点
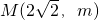
到抛物线的焦点F的距离是3,所以点
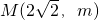
到抛物线的准线
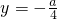
的距离是3,
所以
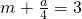
.
所以
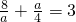
.
所以a=4,或a=8.…..(3分)
因为m>1,所以a=4…(4分)
(Ⅱ)解:由(Ⅰ)知x
2=4y.
因为直线l经过点T(0,1),
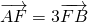
,所以直线l的斜率一定存在,
设直线l的斜率是k,所以直线l的方程是y=kx+1,即kx-y+1=0.
联立方程组
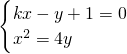
消去y,得x
2-4kx-4=0.…..(5分)
所以
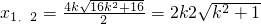
.
因为
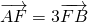
,且k>0,所以
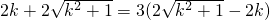
.…..(7分)
所以
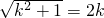
,所以
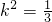
.
因为k>0,所以
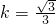
所以k的值是

.…..(8分)
(Ⅲ)证明:由(Ⅱ)知,方程组
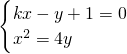
得x
2-4kx-4=0.
设A(x
1,y
1),B(x
2,y
2),所以x
1+x
2=4k,x
1x
2=-4
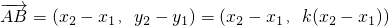
.…..(9分)
由x
2=4y,所以

,所以
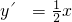
.
所以切线QA的方程是
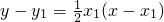
,切线QB的方程是
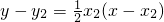
.…..(11分)
所以点Q的坐标是(

,
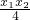
),即(2k,-1),所以
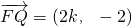
.
因为
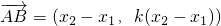
所以
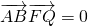
.…..(14分)
分析:(Ⅰ)利用点
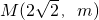
在抛物线C:x
2=ay(a>0)上,点
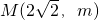
到抛物线的焦点F的距离是3,根据定义,建立方程,从而可求a的值;
(Ⅱ)设直线l的方程与抛物线方程联立,利用
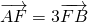
,建立方程,结合k>0,可求k的值;
(Ⅲ)设直线l的方程与抛物线方程联立,确定

的坐标,确定切线QA、QB的方程,求出点Q的坐标,从而可得
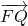
的坐标,利用数量积公式可得结论.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查抛物线的切线方程,考查向量知识的运用,考查学生的计算能力,属于中档题.

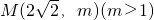 到点F的距离是3.
到点F的距离是3.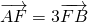 ,求k的值.
,求k的值.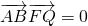 .
.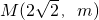 在抛物线C:x2=ay(a>0)上,所以am=8.
在抛物线C:x2=ay(a>0)上,所以am=8.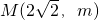 到抛物线的焦点F的距离是3,所以点
到抛物线的焦点F的距离是3,所以点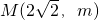 到抛物线的准线
到抛物线的准线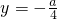 的距离是3,
的距离是3,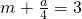 .
.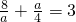 .
.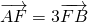 ,所以直线l的斜率一定存在,
,所以直线l的斜率一定存在,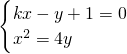 消去y,得x2-4kx-4=0.…..(5分)
消去y,得x2-4kx-4=0.…..(5分)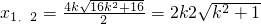 .
.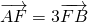 ,且k>0,所以
,且k>0,所以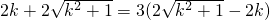 .…..(7分)
.…..(7分)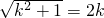 ,所以
,所以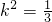 .
.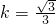
 .…..(8分)
.…..(8分)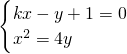 得x2-4kx-4=0.
得x2-4kx-4=0.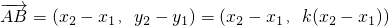 .…..(9分)
.…..(9分) ,所以
,所以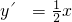 .
.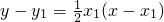 ,切线QB的方程是
,切线QB的方程是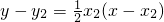 .…..(11分)
.…..(11分) ,
,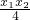 ),即(2k,-1),所以
),即(2k,-1),所以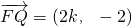 .
.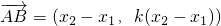
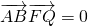 .…..(14分)
.…..(14分)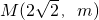 在抛物线C:x2=ay(a>0)上,点
在抛物线C:x2=ay(a>0)上,点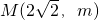 到抛物线的焦点F的距离是3,根据定义,建立方程,从而可求a的值;
到抛物线的焦点F的距离是3,根据定义,建立方程,从而可求a的值;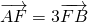 ,建立方程,结合k>0,可求k的值;
,建立方程,结合k>0,可求k的值; 的坐标,确定切线QA、QB的方程,求出点Q的坐标,从而可得
的坐标,确定切线QA、QB的方程,求出点Q的坐标,从而可得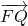 的坐标,利用数量积公式可得结论.
的坐标,利用数量积公式可得结论.
