已知E(2,2)是抛物线C:y2=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N.
(Ⅰ)求抛物线方程及其焦点坐标;
(Ⅱ)已知O为原点,求证:∠MON为定值.
【答案】
分析:(Ⅰ)将E(2,2)代入y
2=2px,得p=1,由此能求出抛物线方程和焦点坐标.
(Ⅱ)设A(

,y
1),B(

,y
2),M(x
M,y
M),N(x
N,y
N),设直线l方程为y=k(x-2),与抛物线方程联立得到ky
2-2y-4k=0,由韦达定理,得y
1y
2=-4,

,由此能够推导出∠MON为定值.
解答:(本小题满分14分)
(Ⅰ)解:将E(2,2)代入y
2=2px,得p=1,
所以抛物线方程为y
2=2x,焦点坐标为(

,0).…(3分)
(Ⅱ)证明:设A(

,y
1),B(
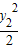
,y
2),M(x
M,y
M),N(x
N,y
N),
因为直线l不经过点E,所以直线l一定有斜率
设直线l方程为y=k(x-2),
与抛物线方程联立得到

,消去x,得:
ky
2-2y-4k=0,
则由韦达定理得:
y
1y
2=-4,

,…(6分)
直线AE的方程为:y-2=
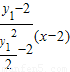
,
即y=

,
令x=-2,得y
M=

,…(9分)
同理可得:

,…(10分)
又∵
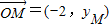
,

,
所以

=4+y
My
N=4+

=4+
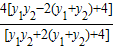
=

=0…(13分)
所以OM⊥ON,即∠MON为定值

…(14分).
点评:本题考查抛物线方程及其焦点坐标的求法,考查角为定值的证明,解题时要认真审题,注意抛物线的简单性质,直线与抛物线的位置关系、韦达定理等知识点的合理运用.

 ,y1),B(
,y1),B( ,y2),M(xM,yM),N(xN,yN),设直线l方程为y=k(x-2),与抛物线方程联立得到ky2-2y-4k=0,由韦达定理,得y1y2=-4,
,y2),M(xM,yM),N(xN,yN),设直线l方程为y=k(x-2),与抛物线方程联立得到ky2-2y-4k=0,由韦达定理,得y1y2=-4, ,由此能够推导出∠MON为定值.
,由此能够推导出∠MON为定值. ,0).…(3分)
,0).…(3分) ,y1),B(
,y1),B(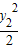 ,y2),M(xM,yM),N(xN,yN),
,y2),M(xM,yM),N(xN,yN), ,消去x,得:
,消去x,得: ,…(6分)
,…(6分)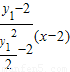 ,
, ,
, ,…(9分)
,…(9分) ,…(10分)
,…(10分)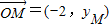 ,
, ,
, =4+yMyN=4+
=4+yMyN=4+
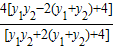
 =0…(13分)
=0…(13分) …(14分).
…(14分).

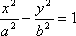 的一个焦
的一个焦![]() 点是抛物线y2=2
点是抛物线y2=2![]() x的焦点,且双曲线C经过点(1,
x的焦点,且双曲线C经过点(1,![]() ),又知直线l:y=kx+1与双曲线C相交于A、B两点.
),又知直线l:y=kx+1与双曲线C相交于A、B两点.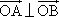 ,求实数k值.
,求实数k值.