
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足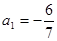 ,
, (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),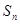 为数列{an}的前
为数列{an}的前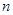 项和.
项和.
(1) 若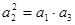 ,求
,求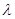 的值;
的值;
(2) 求数列{an}的通项公式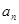 ;
;
(3) 当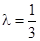 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
(1) ;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。
;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。
解析试题分析:(1) 令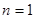 ,得到
,得到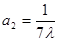 ,令
,令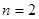 ,得到
,得到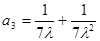 。…………2分
。…………2分
由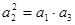 ,计算得
,计算得 .……………………………………………………4分
.……………………………………………………4分
(2) 由题意 ,可得:
,可得: ,所以有
,所以有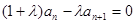
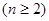 ,又
,又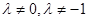 ,……………………5分
,……………………5分
得到: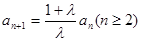 ,故数列
,故数列 从第二项起是等比数列。……………7分
从第二项起是等比数列。……………7分
又因为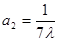 ,所以n≥2时,
,所以n≥2时,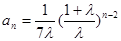 ……………………………8分
……………………………8分
所以数列{an}的通项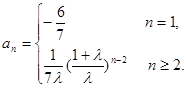 …………………………………10分
…………………………………10分
(3) 因为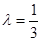 所以
所以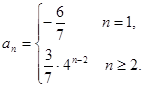 ……………………………………11分
……………………………………11分
假设数列{an}中存在三项am、ak、ap成等差数列,
①不防设m>k>p≥2,因为当n≥2时,数列{an}单调递增,所以2ak=am+ap
即:2´(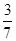 )´4k–2 =
)´4k–2 = 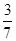 ´4m–2 +
´4m–2 + 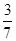 ´4p–2,化简得:2´4k - p= 4m–p+1
´4p–2,化简得:2´4k - p= 4m–p+1
即22k–2p+1=22m–2p+1,若此式成立,必有:2m–2p=0且2k–2p+1=1,
故有:m=p=k,和题设矛盾………………………………………………………………14分
②假设存在成等差数列的三项中包含a1时,
不妨设m=1,k>p≥2且ak>ap,所以2ap = a1+ak ,
2´(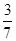 )´4p–2 = –
)´4p–2 = –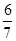 + (
+ (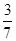 )´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
)´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
因为k > p ≥ 2,所以当且仅当k=3且p=2时成立………………………………………16分
因此,数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列……………………………18分
考点:等差数列的性质;数列通项公式的求法;数列的递推式。
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,还考查了一定的逻辑运算与推理的能力及考查了学生通过已知条件分析问题和解决问题的能力.题目较难。


科目:高中数学 来源: 题型:解答题
各项均为正数的等比数列{an}中,已知a2="8," a4="128," bn=log2an .
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Sn
(3)求满足不等式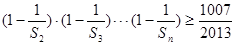 的正整数n的最大值
的正整数n的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设递增等比数列{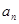 }的前n项和为
}的前n项和为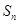 ,且
,且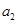 =3,
=3,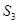 =13,数列{
=13,数列{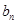 }满足
}满足 =
=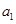 ,点P(
,点P(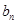 ,
,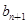 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡.
(Ⅰ)求数列{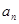 },{
},{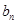 }的通项公式;
}的通项公式;
(Ⅱ)设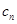 =
=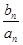 ,数列{
,数列{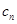 }的前n项和
}的前n项和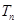 ,若
,若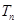 >2a-1恒成立(n∈N﹡),求实数a的取值范围.
>2a-1恒成立(n∈N﹡),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在数列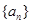 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
.
(1)证明数列 为等差数列,并求
为等差数列,并求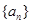 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,求使得
,求使得 的最小正整数
的最小正整数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列, 为
为 的前n项和.(1)求通项公式
的前n项和.(1)求通项公式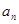 及
及 ;
;
(2)设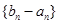 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列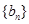 的通项公式及其前n项和
的通项公式及其前n项和
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设数列{an}的前n项和为Sn,点(n, )(n∈N*)均在函数y=
)(n∈N*)均在函数y= x+
x+ 的图象上,则a2014=( )
的图象上,则a2014=( )
| A.2014 | B.2013 | C.1012 | D.1011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com