
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 的最大值;
的最大值;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国古典乐器一般按“八音”分类.“八音”是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼·春官·大师》,分为“金、石、土、革、丝、木、匏(páo)、竹”八音.其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器,现从打击乐器、弹拨乐器中任取不同的‘两音’,含有弹拨乐器的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(1,2)的直线l的参数方程为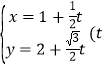 为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
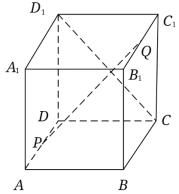
【题目】如图,在正方体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上的动点,下列说法中:
上的动点,下列说法中:
①![]() 可能与平面
可能与平面![]() 平行;
平行;
②![]() 与
与![]() 所成的角的最大值为
所成的角的最大值为![]() ;
;
③![]() 与
与![]() 一定垂直;
一定垂直;
④![]()
⑤![]() 与
与![]() 所成的最大角的正切值为
所成的最大角的正切值为![]() .
.
其中正确个数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过![]() 天,重度污染的天数仅有
天,重度污染的天数仅有![]() 天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取
天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取![]() 户,进行月均用气量调查,得到的用气量数据均在区间
户,进行月均用气量调查,得到的用气量数据均在区间![]() 内,表如下
内,表如下
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求![]() 和
和![]() 值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
(2)从样本调查的用气量![]() 和
和![]() 的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.
的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com