
【题目】如图,在斜三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,均为正三角形,E为AB的中点.
,均为正三角形,E为AB的中点.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求斜三棱柱![]() 截去三棱锥
截去三棱锥![]() 后剩余部分的体积.
后剩余部分的体积.
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
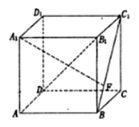
A.无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
B.当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
C.无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
D.当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处有极值,且
处有极值,且![]() ,则称
,则称![]() 为函数
为函数![]() 的“F点”.
的“F点”.
(1)设函数![]() (
(![]() ).
).
①当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
②若函数![]() 存在“F点”,求k的值;
存在“F点”,求k的值;
(2)已知函数![]() (a,b,
(a,b,![]() ,
,![]() )存在两个不相等的“F点”
)存在两个不相等的“F点”![]() ,
,![]() ,且
,且![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是边长为![]() 的等边三角形,
的等边三角形,![]() ,点O,M分别是AB,BC的中点.
,点O,M分别是AB,BC的中点.
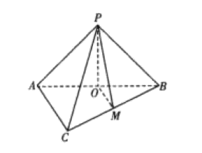
(1)证明:AC//平面POM;
(2)求点B到平面POM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
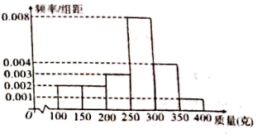
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: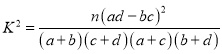 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
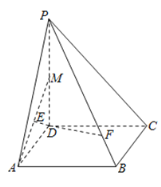
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856310)
已知函数f(x)=x+![]() +ln x(a∈R).
+ln x(a∈R).
(Ⅰ)当a=2时, 求函数f(x)的单调区间;
(Ⅱ)若关于x的函数g(x)=![]() -f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
-f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com