
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,曲线
时,曲线![]() 总在曲线
总在曲线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2) ![]() .
.
【解析】试题分析:(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(2)原命题等价于不等式
的减区间;;(2)原命题等价于不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,不等式
,不等式![]() 恒成立,可化为
恒成立,可化为![]() 恒成立,只需
恒成立,只需![]() 大于
大于![]() 的最大值即可.
的最大值即可.
试题解析:(1)由![]() 可得
可得![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
若![]() ,则
,则![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)原命题等价于不等式![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,不等式
,不等式![]() 恒成立.
恒成立.
∵当![]() 时,
时,![]() ,∴
,∴![]() ,
,
即证当![]() 时,
时,![]() 大于
大于![]() 的最大值.
的最大值.
又∵当![]() 时,
时,![]() ,∴
,∴![]() ,
,
综上所述,![]() .
.
【方法点晴】本题主要考查利用导数研究函数的单调性以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 即可)或
即可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ① 求得
恒成立;④ 讨论参数.本题是利用方法 ① 求得![]() 的范围.
的范围.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)如果存在过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与
与![]() 的倾斜角互补,求实数
的倾斜角互补,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,E为PA的中点,F为BC的中点,底面ABCD是菱形,对角线AC,BD交于点O.求证:
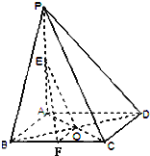
(1)平面EFO∥平面PCD;
(2)平面PAC⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某重点中学100位学生在市统考中的理科综合分数,以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求理科综合分数的众数和中位数;
(3)在理科综合分数为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在
的四组学生中,用分层抽样的方法抽取11名学生,则理科综合分数在![]() 的学生中应抽取多少人?
的学生中应抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com