
| A+B |
| 2 |
| 2 |
| A+B |
| 2 |
| ||
| 2 |
| A+B |
| 2 |
sin
| ||
cos
|
| A+B |
| 2 |
| A+B |
| 2 |
| A+B |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
| AD |
| BC |
| AH |
| HD |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:南通高考密卷·数学(理) 题型:013
在△ABC中,已知三边a,b,c成等差数列,且有sinB+cosB=t,则t的取值范围是
[ ]
 )
) )
) ,+∞)
,+∞)查看答案和解析>>
科目:高中数学 来源:上杭一中、武平一中、长汀一中、漳平一中2006-2007学年第一学期高三期末考数学试题(理) 题型:044
在△ABC中,已知B(-3,0),C(3,0),D为线段BC上一点,![]() 是△ABC的垂心,且
是△ABC的垂心,且![]() .
.
(1)求点H的轨迹M的方程;
(2)若过C点且斜率为![]() 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,
求:当△CPQ为锐角三角形时t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2004年江苏省无锡市高三调研数学试卷(解析版) 题型:解答题
 ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.查看答案和解析>>
科目:高中数学 来源:江苏省陆慕高级中学09-10学年高二上学期第一次测试 题型:解答题
在△ABC中,已知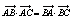 .
.
(Ⅰ) 求证: | |=|
|=| |;
|;
(Ⅱ) 若| +
+ |=|
|=| -
- |=
|= ,求|
,求| -t
-t |的最小值以及相应的t的值.
|的最小值以及相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com