
���� ����f��x����ͼ������$\frac{f��{x}_{1}��}{{x}_{1}}$=$\frac{f��{x}_{2}��}{{x}_{2}}$=��=$\frac{f��{x}_{n}��}{{x}_{n}}$=k�ļ��������ǹ�ԭ���ֱ����f��x���ཻ���б�ʣ��������ν�Ͻ�����⼴�ɣ�
��� 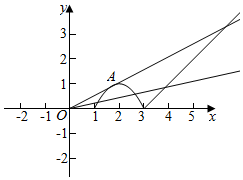 �⣺��������f��x����ͼ����ͼ��$\frac{f��{x}_{1}��}{{x}_{1}}$=$\frac{f��{x}_{2}��}{{x}_{2}}$=��=$\frac{f��{x}_{n}��}{{x}_{n}}$=k�ļ��������ǹ�ԭ���ֱ����f��x���ཻ���б�ʣ�
�⣺��������f��x����ͼ����ͼ��$\frac{f��{x}_{1}��}{{x}_{1}}$=$\frac{f��{x}_{2}��}{{x}_{2}}$=��=$\frac{f��{x}_{n}��}{{x}_{n}}$=k�ļ��������ǹ�ԭ���ֱ����f��x���ཻ���б�ʣ�
��ͼ��֪��ԭ���ֱ�ߺ�f��x�������3�����㣬��n�����ֵ��3��
��n=2����ֱ����f��x�����������㣬
��ԭ���ֱ��y=kx��б��k=0������y=kx��f��x����1��x��3����ʱ��б�ʣ�
����$\frac{f��{x}_{n}��}{{x}_{n}}$�����ֵΪy=kxf��x����1��x��3����ʱ��б�ʣ�
��y=kx����y=-x2+4x-3����kx=-x2+4x-3����x2+��k-4��x+3=0��
���б�ʽ��=��k-4��2-12=0��k-4=��$2\sqrt{3}$����k=4��$2\sqrt{3}$��
�߷��̵ĸ�x=$-\frac{k-4}{2}$�ʣ�1��2����
��0��k��2����k=4-$2\sqrt{3}$��
��$\frac{f��{x}_{n}��}{{x}_{n}}$�����ֵ����4-$2\sqrt{3}$��
�ʴ�Ϊ��3��4-$2\sqrt{3}$
���� ������Ҫ����ֶκ�����Ӧ�ã���ȷ����$\frac{f��{x}_{1}��}{{x}_{1}}$=$\frac{f��{x}_{2}��}{{x}_{2}}$=��=$\frac{f��{x}_{n}��}{{x}_{n}}$=k�ļ��������ǹ�ԭ���ֱ����f��x���ཻ���б�ʣ��ǽ������Ĺؼ���ע���������ν�Ͻ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
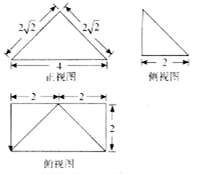 ��֪����P-ABCD������ͼ��ͼ��ʾ��������������İ뾶Ϊ��������
��֪����P-ABCD������ͼ��ͼ��ʾ��������������İ뾶Ϊ��������| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$ | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
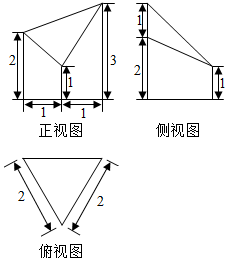
| A�� | 2$\sqrt{2}$ | B�� | 2$\sqrt{3}$ | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
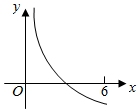
| A�� | f�䣨3����f�䣨4����f��4��-f��3����0 | B�� | f�䣨3����f��4��-f��3����f�䣨4����0 | C�� | f�䣨4����f��4��-f��3����f�䣨3����0 | D�� | f��4��-f��3����f�䣨4����f�䣨3����0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com