
分析 方法一:(Ⅰ)利用正弦定理、诱导公式、两角和的正弦公式化简已知的式子,由内角的范围和特殊角的三角函数值求出角C;
(Ⅱ)利用余弦定理列出方程,由条件和完全平方公式化简后,利用基本不等式求出c的最小值,由面积公式求出△ABC的面积;
方法二:(Ⅰ)利用余弦定理化简已知的式子得到边的关系,由余弦定理求出cosC的值,由内角的范围和特殊角的三角函数值求出角C;
(Ⅱ)利用余弦定理列出方程,结合条件消元后,利用一元二次函数的性质求出c的最小值,由面积公式求出△ABC的面积.
解答 解:方法一:(Ⅰ)∵2ccosA+a=2b,
∴2sinCcosA+sinA=2sinB,…(1分)
∵A+B+C=π,
∴2sinCcosA+sinA=2sin(A+C),…(2分)
即 2sinCcosA+sinA=2sinAcosC+2cosAsinC,…(3分)
∴sinA=2sinAcosC,…(4分)
∵sinA≠0,∴cosC=$\frac{1}{2}$,…(5分)
又∵C是三角形的内角,∴C=$\frac{π}{3}$. …(6分)
(Ⅱ)由余弦定理得:c2=a2+b2-2abcosC=a2+b2-ab,…(7分)
∵a+b=4,故c2=a2+b2-ab=(a+b)2-3ab=16-3ab,…(8分)
∴${c^2}=16-3ab≥16-3{(\frac{a+b}{2})^2}=4$(当且仅当a=b=2时等号成立),…(10分)
∴c的最小值为2,故${S_{△ABC}}=\frac{1}{2}absinC=\sqrt{3}$.…(12分)
方法二:(Ⅰ)∵2ccosA+a=2b,
∴$2c•\frac{{{b^2}+{c^2}-{a^2}}}{2bc}+a=2b$,…(1分)
∴b2+c2-a2+ab=2b2,即 c2=a2+b2-ab,…(3分)
∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,…(5分)
又∵C是三角形的内角,∴c=$\frac{π}{3}$. …(6分)
(Ⅱ)由已知,a+b=4,即b=4-a,
由余弦定理得,c2=a2+b2-ab=(a+b)2-3ab,…(8分)
∴c2=16-3a(4-a)=3(a-2)2+4,…(10分)
∴当a=2时,c的最小值为2,故${S_{△ABC}}=\frac{1}{2}absinC=\sqrt{3}$. …(12分)
点评 本题考查正弦、余弦定理,三角恒等变换中的公式,以及求最值的方法:基本不等式、一元二次函数的性质,考查一题多解,化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
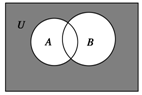 设全集U=R,A={x|y=lg(2x-x2)},B={y|y=cos x},则图中阴影部分表示的区间是( )
设全集U=R,A={x|y=lg(2x-x2)},B={y|y=cos x},则图中阴影部分表示的区间是( )| A. | [-1,2) | B. | (-1,2) | C. | (-∞,-1)∪[2,+∞) | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 4 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,2) | B. | (7,-14) | C. | (7,-4) | D. | (7,-8) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x,g(x)=\sqrt{x^2}$ | B. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x+1$ | ||
| C. | $f(x)=x,g(x)=\root{3}{x^3}$ | D. | $f(x)=|x|,\;g(x)={(\sqrt{x})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com