
分析 设A,B均为锐角,推导出C也为锐角,可判断(1);求出f(cos$\frac{π}{6}$)的值,可判断(2);根据正弦函数的对称性,可判断(3);画出函数f(x)的图象,并判断其与y=lg|x|图象交点的个数,可判断(4).
解答 解:由题意可得A,B,C不能为直角,故可设A,B均为锐角,
又tanA+tanB+tanC=tan(A+B)(1-tanA•tanB)+tanC=-tanC(1-tanAtanB)+tanC=tanA•tanB•tanC>0,
∴tanC>0,tanA>0,tanB>0,或一正、二负(舍),即A、B、C均为锐角,
故△ABC为锐角三角形,
故(1)正确.
∵f(sinx+cosx)=sinxcosx=$\frac{(sinx+cosx)^{2}-1}{2}$,
故f(x)=$\frac{{x}^{2}-1}{2}$,
故f(cos$\frac{π}{6}$)=f($\frac{\sqrt{3}}{2}$)=-$\frac{1}{8}$,
故(2)错误;
当x=$\frac{π}{8}$时,y=sin(2x+$\frac{5π}{4}$)取最小值,
故x=$\frac{π}{8}$是函数y=sin(2x+$\frac{5π}{4}$)的一条对称轴方程,
故(3)正确;
(4)∵f(x+$\frac{π}{2}$)=f(x-$\frac{π}{2}$);
∴函数f(x)的周期为π,
∵当x∈(0,π]时,f(x)=-cosx,
∴函数f(x)的图象如下图所示: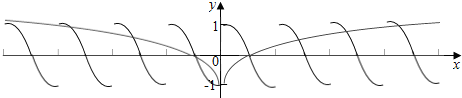
由图可得:两函数图象共有8个交点,
即方程f(x)=lg|x|解的个数是8个.
故(4)正确;
故答案为:(1)(3)(4)
点评 本题考查的知识点是命题的真假故判断与应用,数形结合思想,三角函数的图象和性质,难度中档.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (0,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com