
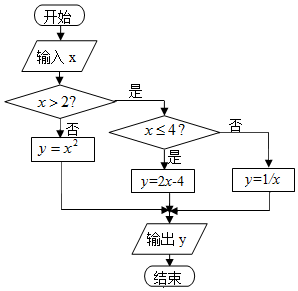
 阅读程序框图,回答以下问题:
阅读程序框图,回答以下问题:分析 (1)根据已知中程序框图的分支条件及各分支上对应的操作,可得分段函数f(x)的解析式;
(2)分类讨论输出的结果相等时,输入的x值,最后综合讨论结果,可得答案.
(3)先判定循环的结构,然后选择对应的循环语句,对照流程图进行逐句写成语句即可
解答 解:(1)该程序框图表达的函数解析式是y=$\left\{\begin{array}{l}{{x}^{2},x≤2}\\{2x-4,2<x≤4}\\{\frac{1}{x},x>4}\end{array}\right.$
(2)在各自范围内分别求可得,
当x≤2时,x2=x,解得x=0,或x=1,
当2<x≤4时,2x-4=x,解得x=4,
当x>4时,$\frac{1}{x}$=x,解得x=±1(舍去)
所以这样的x有3个,分别为0,1,4
(3)条件语句
INPUT x
IF x<=2,THEN
y=x2
ELSE
IF x>4,THEN
y=1/x
ELSE
y=2*4-4
END IF
END IF
PRINT y
END
点评 本题考查的知识点是选择结构,分段函数,考查了循环结构的程序框图的应用,考查了将直到型循环结构的流程图转化成算法语句,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
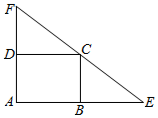 某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线.
某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com