
分析 (1)利用不等式的性质进行证明;
(2)利用定积分的几何意义求封闭图形的面积.
解答 (1)证明:∵$\sqrt{a}>\sqrt{a-2},\sqrt{a-1}>\sqrt{a-3}$
∴$\sqrt{a}+\sqrt{a-1}>\sqrt{a-2}+\sqrt{a-3}$
∴$\frac{1}{\sqrt{a}+\sqrt{a-1}}<\frac{1}{\sqrt{a-2}+\sqrt{a-3}}$
∴$\sqrt{a}-\sqrt{a-1}<\sqrt{a-2}-\sqrt{a-3}$ (6分)
(2)解:联立方程$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y=x-2}\end{array}\right.$得到两曲线的交点(4,2),
因此由曲线y=$\sqrt{x}$,直线y=x-2及y轴所围成的图形的面积为S=${∫}_{0}^{4}(\sqrt{x}-x+2)dx$=$\frac{2}{3}{x}^{\frac{3}{2}}-\frac{1}{2}{x}^{2}+{2x}^{\;}{|}_{0}^{4}$=$\frac{16}{3}$ (12分)
点评 本题考查了不等式性质的运用证明不等式以及利用定积分求封闭图形的面积.(1)也可以利用分析法证明.(2)关键是利用定积分表示围成的图形面积.


科目:高中数学 来源: 题型:选择题
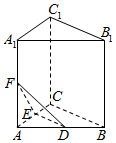 如图,三棱柱A1B1C1-ABC中,已知D,E,F分别为AB,AC,AA1的中点,设三棱锥A-FED的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1:V2的值为( )
如图,三棱柱A1B1C1-ABC中,已知D,E,F分别为AB,AC,AA1的中点,设三棱锥A-FED的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1:V2的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
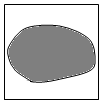 如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒100粒豆子,落在阴影区域内的豆子共60粒,据此估计阴影区域的面积为$\frac{12}{5}$.
如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒100粒豆子,落在阴影区域内的豆子共60粒,据此估计阴影区域的面积为$\frac{12}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
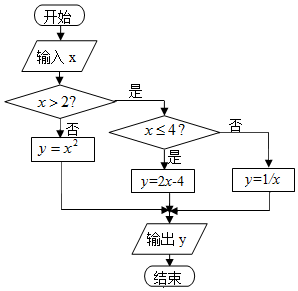 阅读程序框图,回答以下问题:
阅读程序框图,回答以下问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+3y-7=0 | B. | 2x+3y-1=0 | C. | 2x-3y+1=0 | D. | 2x-3y+7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3x-3 | B. | y=$\frac{1}{3}$x-$\frac{1}{3}$ | C. | y=-$\frac{1}{3}$x+$\frac{1}{3}$ | D. | y=-3x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂直 | B. | 不垂直也不平行 | C. | 平行且同向 | D. | 平行且反向 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com