Question

8．A是半径为2的圆O内一个定点，P是圆O上的一个动点，线段AP的垂直平分线l与半径OP相交于点Q，则|OQ|•|QA|的最大值为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由已知得|OQ|+|QA|=|OQ|+|QP|=|OP|=2，从而2=|OQ|+|QA|≥2$\sqrt{|OQ|•|QA|}$，由此能求出|OQ|•|QA|的最大值．

解答 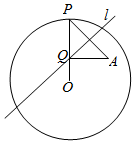解：∵A是半径为2的圆O内一个定点，P是圆O上的一个动点，
线段AP的垂直平分线l与半径OP相交于点Q，
∴|OQ|+|QA|=|OQ|+|QP|=|OP|=2，∴2=|OQ|+|QA|≥2$\sqrt{|OQ|•|QA|}$，
∴|OQ|•|QA|≤1，
当且仅当Q为OP中点时取等号，
∴|OQ|•|QA|的最大值为1．
故选：A．

点评 本题考查两线段积的最大值的求法，是中档题，解题时要认真审题，注意圆形结合思想、均值定理的合理运用．