
分析 由条件利用同角三角函数的基本关系,二倍角公式,把函数的解析式化为y=$\frac{{2sin}^{2}\frac{θ}{2}+{2cos}^{2}\frac{θ}{2}-2sin\frac{θ}{2}cos\frac{θ}{2}}{1-(1-{2cos}^{2}\frac{θ}{2})}$=${(cot\frac{θ}{2}-\frac{1}{2})}^{2}$+$\frac{3}{4}$,再利用二次函数的性质求得它的最小值.
解答 解:y=$\frac{2-sinθ}{1-cosθ}$=$\frac{{2sin}^{2}\frac{θ}{2}+{2cos}^{2}\frac{θ}{2}-2sin\frac{θ}{2}cos\frac{θ}{2}}{1-(1-{2cos}^{2}\frac{θ}{2})}$=$\frac{{tan}^{2}\frac{θ}{2}+1-tan\frac{θ}{2}}{{tan}^{2}\frac{θ}{2}}$=${cot}^{2}\frac{θ}{2}$-cot$\frac{θ}{2}$+1=${(cot\frac{θ}{2}-\frac{1}{2})}^{2}$+$\frac{3}{4}$,
故当cot$\frac{θ}{2}$=$\frac{1}{2}$时,函数y取得最小值为$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式,二次函数的性质的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
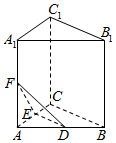 如图,三棱柱A1B1C1-ABC中,已知D,E,F分别为AB,AC,AA1的中点,设三棱锥A-FED的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1:V2的值为( )
如图,三棱柱A1B1C1-ABC中,已知D,E,F分别为AB,AC,AA1的中点,设三棱锥A-FED的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1:V2的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
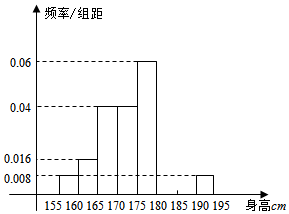 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第七组的人数为3人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第七组的人数为3人.| 喜欢打篮球 | 不喜欢打篮球 | 总计 | |
| 身高超过175cm | 20 | 6 | 26 |
| 身高不超175cm | 5 | 19 | 24 |
| 总计 | 25 | 25 | 50 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com