
分析 设P(x,y),由PA=2PT,把原题转化为直线3x+4y-a=0与圆${({x-\frac{1}{3}})^2}+{y^2}=\frac{16}{9}$有公共点,由此能求出a的最大值.
解答 解:设P(x,y),由PA=2PT,得(x+1)2+y2=4(x2+y2-1),
化简得${({x-\frac{1}{3}})^2}+{y^2}=\frac{16}{9}$,
转化为直线3x+4y-a=0与圆${({x-\frac{1}{3}})^2}+{y^2}=\frac{16}{9}$有公共点,
所以$d=\frac{{|{1-a}|}}{5}≤\frac{4}{3}$,
解得$-\frac{17}{3}≤a≤\frac{23}{3}$.
∴a的最大值为$\frac{23}{3}$.
故答案为:$\frac{23}{3}$.
点评 本题考查实数值的最大值的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
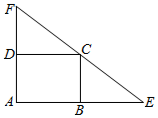 某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线.
某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥α且n∥α,则m∥n | B. | m∥α且 m∥β,则α∥β | ||
| C. | α∥β且 m?α,n?β,则m∥n | D. | α∥β且 a?α,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com