
| A. | m∥α且n∥α,则m∥n | B. | m∥α且 m∥β,则α∥β | ||
| C. | α∥β且 m?α,n?β,则m∥n | D. | α∥β且 a?α,则a∥β |
分析 根据空间线面位置关系的判定定理进行判断或举反例说明.
解答 解:对于A,∵m∥α,n∥α,∴存在直线m′?α,n′?α,使得m∥m′,n′∥n,
若m′,n′为相交直线,则m,n不平行,故A错误.
对于B,若α∩β=l,m∥l,且m?α,m?β,显然有m∥α,m∥β,故B错误.
对于C,以长方体ABCD-A′B′C′D′为例,则平面ABCD∥平面A′B′C′D′,
显然AB?平面ABCD,B′C′?平面A′B′C′D′,AB与B′C′不平行,故C错误.
对于D,若α∥β且 a?α,则a与平面β没有公共点,∴a∥β.故D正确.
故选D.
点评 本题考查了空间线面位置关系的判定,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{9}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | $\frac{64π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
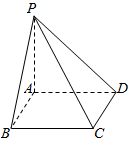 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com