
分析 (1)由二次函数的图象和性质得到对称轴,由此得到未知量.
(2)由题意得到三个不等式,由函数y=ax+b在[-1,1]上单调,利用绝对值不等式的性质得到结论.
解答 解:(1)∵函数y=f(x)的图象过原点,
∴c=0
∵|f(x)|≤1的解集为{x|-1≤x≤3},
得到f(x)对称轴为x=1
得:b=-2a
∵|f(-1)|=1,|f(3)|=1
∴$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{2}{3}}\end{array}\right.$
∴f(x)的解析式是f(x)=$\frac{1}{3}$x2-$\frac{2}{3}$x或f(x)=-$\frac{1}{3}$x2+$\frac{2}{3}$x或
证明:(2)由题意得,|f(0)=|c|≤1|
|f(1)|=|a+b+c|≤1
|f(-1)|=|a-b+c|≤1|
∵函数y=ax+b在[-1,1]上单调,
∴|ax+b|≤max{|a+b|,|-a+b|}
又∵|a+b|≤|a+b+c|+|-c|≤2
|a-b|≤|a-b+c|+|-c|≤2
∴|ax+b|≤2.
点评 本题考查不等式的证明,涉及绝对值不等式的性质,函数的单调性.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,x2>0”为真命题 | |
| C. | 命题“若x=y,则cosx=cosy”的逆否命题为真命题 | |
| D. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥α且n∥α,则m∥n | B. | m∥α且 m∥β,则α∥β | ||
| C. | α∥β且 m?α,n?β,则m∥n | D. | α∥β且 a?α,则a∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16π}{3}$ | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
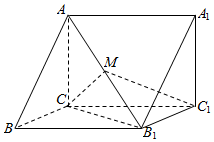 如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.
如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com