
分析 由等差中项的性质列出等式并表示出c,由点到直线的距离公式求出圆心到直线l的距离平方,由$\frac{{a}^{2}+{b}^{2}}{2}≥(\frac{a+b}{2})^{2}$求出距离平方的范围,根据弦长公式求出所截得弦长的最小值,由直线过圆心求出最大值,即可求出所截得弦长的取值范围.
解答 解:∵实数c是a,b的等差中项,∴2c=a+b,则c=$\frac{a+b}{2}$,
∴圆心(0,0)到直线l:ax-by+c=0的距离平方:d2=${(\frac{|c|}{\sqrt{{a}^{2}+{b}^{2}}})}^{2}$=$\frac{(\frac{a+b}{2})^{2}}{{a}^{2}+{b}^{2}}$,
∵$\frac{{a}^{2}+{b}^{2}}{2}≥(\frac{a+b}{2})^{2}$,∴d2$≤\frac{1}{2}$,当且仅当a=b时取等号,
∴直线l被圆x2+y2=9所截得弦长是:2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{9-{d}^{2}}$$≥2\sqrt{9-\frac{1}{2}}$=$\sqrt{34}$,
∵当直线l过圆心(0,0)时,所得的弦长最大是直径为6,
∴所截得弦长的取值范围是$[\sqrt{34},6]$,
故答案为:$[\sqrt{34},6]$.
点评 本题考查直线与圆的位置关系,点到直线的距离公式,弦长公式,以及利用不等式求最值,属于中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{12}{5}$,0] | B. | [0,$\frac{5}{12}$] | C. | [0,$\frac{4}{3}$] | D. | (0,$\frac{12}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±2$\sqrt{2}$ | B. | ±$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
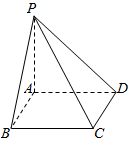 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | (-∞,1] | C. | [3,+∞) | D. | [$\frac{3}{2}$,$\frac{11}{6}}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com