
| A. | [-$\frac{12}{5}$,0] | B. | [0,$\frac{5}{12}$] | C. | [0,$\frac{4}{3}$] | D. | (0,$\frac{12}{5}$) |
分析 圆心为(2,0),由题意知(2,0)到直线l:mx-y-1=0的距离不大于1,由此能求出实数m的取值范围.
解答 解:圆C:x2+y2-4x+3=0的标准方程为(x-2)2+y2=1,
圆心为C(2,0),
∵直线l:mx-y-1=0与圆C:x2+y2-4x+3=0有公共点,
∴由题意知C(2,0)到直线l:mx-y-1=0的距离不大于1,
即$\frac{|2m-1|}{\sqrt{{m}^{2}+1}}$≤1,
解得0$≤m≤\frac{4}{3}$.
∴实数m的取值范围是[0,$\frac{4}{3}$].
故选:C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意圆的性质和点到直线的距离公式的合理运用.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{16π}{3}$ | B. | $\frac{4π}{3}$ | C. | π | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
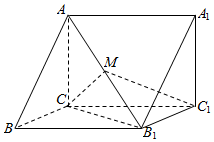 如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.
如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | [0,100] | [100,200] | [200,300] | [300,400] |
| 日销售量等级 | 差 | 中 | 良 | 优秀 |
| 天数 | 20 | 45 | 20 | 15 |
| 非优秀 | 优秀 | 总计 | |
| 夏季 | |||
| 非夏季 | |||
| 总计 | 100 |
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com