
���� ����������������������������ʽ���$\overrightarrow{a}•\overrightarrow{b}$�Լ�|$\overrightarrow a$||$\overrightarrow b$���ɵý��ۣ������û�������ʽ���Ҫ��ʽ�ӵ���Сֵ��ע��1�Ĵ�����$\frac{{a}^{2}}{6}$+$\frac{{2b}^{2}}{3}$+$\frac{{3c}^{2}}{2}$=1��
��� �⣺��$\overrightarrow{a}•\overrightarrow{b}$=x1•x2 +y1•y2 +z1•z2 =$\sqrt{{{{��x}_{1}•x}_{2}��}^{2}{+{��y}_{1}{•y}_{2}��}^{2}{+{��z}_{1}{•z}_{2}��}^{2}}$��|$\overrightarrow a$||$\overrightarrow b$|=$\sqrt{{{x}_{1}}^{2}{{+y}_{1}}^{2}{{+z}_{1}}^{2}}$•$\sqrt{{{x}_{2}}^{2}{{+y}_{2}}^{2}{{+z}_{2}}^{2}}$��
�֡�|$\overrightarrow a$•$\overrightarrow b$|��|$\overrightarrow a$||$\overrightarrow b$|�����ҽ���$\overrightarrow a��\;\;\overrightarrow b$����ʱȡ�Ⱥţ���$\sqrt{{{{��x}_{1}•x}_{2}��}^{2}{+{��y}_{1}{•y}_{2}��}^{2}{+{��z}_{1}{•z}_{2}��}^{2}}$��$\sqrt{{{x}_{1}}^{2}{{+y}_{1}}^{2}{{+z}_{1}}^{2}}$•$\sqrt{{{x}_{2}}^{2}{{+y}_{2}}^{2}{{+z}_{2}}^{2}}$��
���ҽ���$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$ ʱ���Ⱥų�����
��a2+4b2+9c2=6����$\frac{{a}^{2}}{6}$+$\frac{{2b}^{2}}{3}$+$\frac{{3c}^{2}}{2}$=1����$\frac{1}{a^2}$+$\frac{1}{b^2}$+$\frac{1}{c^2}$=�� $\frac{1}{6}$+$\frac{{2b}^{2}}{{3a}^{2}}$+$\frac{{3c}^{2}}{{2a}^{2}}$ ��+��$\frac{{a}^{2}}{{6b}^{2}}$+$\frac{2}{3}$+$\frac{{3c}^{2}}{{2b}^{2}}$��+��$\frac{{a}^{2}}{{6c}^{2}}$+$\frac{{2b}^{2}}{{3c}^{2}}$+$\frac{3}{2}$��
=$\frac{7}{3}$+2$\sqrt{\frac{{2b}^{2}}{{3a}^{2}}•\frac{{a}^{2}}{{6b}^{2}}}$+2$\sqrt{\frac{{3c}^{2}}{{2a}^{2}}•\frac{{a}^{2}}{{6c}^{2}}}$+2$\sqrt{\frac{{3c}^{2}}{{2b}^{2}}•\frac{{2b}^{2}}{{3c}^{2}}}$=6�����ҽ���$\frac{a}{\sqrt{6}}$=$\frac{b}{\sqrt{\frac{3}{2}}}$=$\frac{c}{\sqrt{\frac{2}{3}}}$=$\frac{1}{3}$ʱ��ȡ�Ⱥţ�
�ʴ�Ϊ��$\sqrt{{{{��x}_{1}•x}_{2}��}^{2}{+{��y}_{1}{•y}_{2}��}^{2}{+{��z}_{1}{•z}_{2}��}^{2}}$��$\sqrt{{{x}_{1}}^{2}{{+y}_{1}}^{2}{{+z}_{1}}^{2}}$•$\sqrt{{{x}_{2}}^{2}{{+y}_{2}}^{2}{{+z}_{2}}^{2}}$��$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$=$\frac{{z}_{1}}{{z}_{2}}$��6��
���� ������Ҫ�������������������������㣬��������ʽ��Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | $\frac{1}{2}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
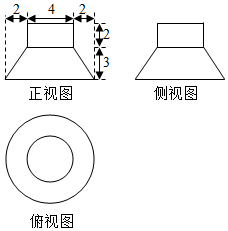 ij�����������ͼ��ͼ��ʾ����˼����������ǣ�������
ij�����������ͼ��ͼ��ʾ����˼����������ǣ�������| A�� | 28�� | B�� | 32�� | C�� | 36�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2=8x | B�� | x2=8y | C�� | y2=4x | D�� | x2=4y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������������ӣ�Ƶ��һ���Խ��Խ�ӽ����� | |
| B�� | Ƶ���ǿ۴��ڵģ������������ | |
| C�� | ����������ģ�������ǰ����ȷ�� | |
| D�� | Ƶ�ʾ��Ǹ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com