
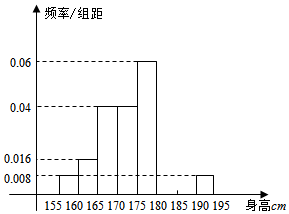
 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第七组的人数为3人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第七组的人数为3人.| 喜欢打篮球 | 不喜欢打篮球 | 总计 | |
| 身高超过175cm | 20 | 6 | 26 |
| 身高不超175cm | 5 | 19 | 24 |
| 总计 | 25 | 25 | 50 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)求出第七组的频率,即可求第六组的频率;
(Ⅱ)分别求出身高在[180,185)内和在[190,195)的人数,标号后利用列举法写出从中随机抽取两名男生的所有情况,查出满足|x-y|≤5的事件个数,然后利用古典概型概率计算公式求解;
(Ⅲ)求出K2,与临界值比较,即可得出结论.
解答 解:(Ⅰ)由题意,第七组的频率为$\frac{3}{50}$=0.06
∴第六组的频率为1-0.06-5×(0.008×2+0.016+0.04×2+0.06)=0.08;
(Ⅱ)在[180,185]内的人数为0.08×50=4人,设为a,b,c,d.身高在[190,195]的人数为0.008×5×50=2人,设为A,B.
若x,y∈[180,185]时,有ab,ac,ad,bc,bd,cd共六种情况.
若x,y∈[190,195]时,有AB共一种情况.
若x,y分别在[180,185],[190,195]内时,有aA,bA,cA,dA,aB,bB,cB,dB共8种情况
所以基本事件的总数为6+8+1=15种,
事件|x-y|≤5所包含的基本事件个数有6+1=7种,故满足|x-y|≤5的事件概率P(E)=$\frac{7}{15}$;
(Ⅲ)由题意,K2=$\frac{50×(20×19-5×6)^{2}}{25×25×26×24}$≈15.705>10.828,
∴有99.9%的把握认为喜欢打篮球和身高超过175cm有关系.
点评 本题考查了频率分布直方图,考查了古典概型及其概率计算公式,考查独立性检验知识的运用,考查了学生的读图能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(1,+∞) | B. | (-2,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | C. | (-2,1) | D. | (-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com