练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．若两直线a、b与面α所成的角相等，则a与b的位置关系是平行或相交或异面．

    分析 不妨设直线a、b与面α所成的角为0°，则a，b与平面α平行或a，b在平面α上，从而得出a，b的位置关系．

    解答 解：假设直线a、b与面α所成的角均为0°，则a，b在平面α上，或a，b与α平行．
    若a?α，b?α，则a，b平行或相交．
    若a?α，b?α，则a∥b或a与b异面．
    故答案为：平行或相交或异面．

    点评 本题考查了空间直线的位置关系，直线与平面所成的角，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．（文科做）$\overrightarrow m$=（$\sqrt{3}$sinx，cosx），$\overrightarrow n$=（3$\sqrt{3}$，1），且$\overrightarrow m$∥$\overrightarrow n$，则$\frac{sin2x}{1+cos2x}$的值为（　　）
    A．2B．3C．4D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

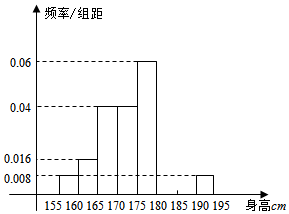    4．从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第七组的人数为3人．
    （Ⅰ）求第六组的频率；
    （Ⅱ）若从身高属于第六组和第八组的所有男生中随机抽取2人，记他们的身高分别为x，y，事件E={|x-y|≤5}，求事件E的频率P（E）；
    （Ⅲ）对抽取的50名学生作调查，得到以下2×2列联表：
    喜欢打篮球不喜欢打篮球总计
    身高超过175cm20626
    身高不超175cm51924
    总计252550
    根据此表判断是否有99.9%的把握认为喜欢打篮球和身高超过175cm有关系．
    参考公式：：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=（a+b）（c+d）（a+c）（b+d））
    参考数据：
    P（K2≥k）0.500.400.250.150.100.050.0250.0100.0050.001
    k0.4550.7081.3232.7022.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知正三角形ABC边长为2，将它沿高AD翻折，使点B与点C间的距离为$\sqrt{3}$，此时四面体ABCD的外接球的表面积为7π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．A是半径为2的圆O内一个定点，P是圆O上的一个动点，线段AP的垂直平分线l与半径OP相交于点Q，则|OQ|•|QA|的最大值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如表为吸烟与患病之间的二联表：
    患病（人数）不患病（人数）合计
    吸烟（人数）aba+b
    不吸烟（人数）cdc+d
    合计a+cb+dn=a+b+c+d
    根据如表，回答下列问题：
    （Ⅰ）试根据上表，用含a，b，c，d，n的式子表示人群中患病的频率为$\frac{a+c}{n}$；在（a+b）个人中患病的频数为$\frac{（a+b）（a+c）}{n}$；在（a+b）个人中不患病的频数为$\frac{（a+b）（b+d）}{n}$；在（c+d）个人中患病的频数为$\frac{（a+c）（c+d）}{n}$；在（c+d）人中不患病的频数为$\frac{（b+d）（c+d）}{n}$．
    （Ⅱ）根据χ2=$\frac{n（ad-bc）^{2}}{（a+b）（b+d）（c+d）（a+c）}$以及临界值表，若a=40，b=10，c=30，d=20，能否有97.5%以上的把握认为吸烟与患病有关？
    P（χ2≥χ0）0.50.40.250.150.10
    χ00.4550.7081.3232.7022.706
    P（χ2≥χ0）0.050.0250.0100.0050.001
    χ03.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．如图，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒100粒豆子，落在阴影区域内的豆子共60粒，据此估计阴影区域的面积为$\frac{12}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若直线的参数方程为$\left\{\begin{array}{l}x=2-3t\\ y=1+2t\end{array}\right.$（t为参数），则直线的普通方程为（　　）
    A．2x+3y-7=0B．2x+3y-1=0C．2x-3y+1=0D．2x-3y+7=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数y=a2-x+1（a＞0，且a≠1）的图象恒过定点A，点A在直线mx+ny=1（mn＞0）上，求$\frac{1}{m}$+$\frac{1}{n}$的最小值．

    查看答案和解析>>

    同步练习册答案