
���� �����⣬���ٴ��붨�弴�ɣ�������ֵf��0��=1����ʹ֮Ϊ�����н纯���������÷�֤�����������ǡ����н纯������֤�����費������������֪���������|f��x��|��M|x|����ʽ���ҵ�M���ɣ�
��� �⣺�����⣺
��Ϊ���У�f��x��=x������|f��x��|��M|x|��|x|��M|x|�����Զ�������M��1����ʹ�����������Ԣ��ǡ����н纯������
��Ϊ���У���x=0ʱ��f��0��=1�����Բ���������M��0ʹ|f��0��|��M|0|�����Ԣڲ��ǡ����н纯������
��Ϊ���У���f��x���ǡ����н纯����������ڳ���M��0��ʹ|x2|��M|x|����|x|��M��һ��x��R��������Ȼ������Mʹ����������Լ��費��������f��x�����ǡ����н纯������
����Ϊf��x���Ƕ�����ʵ����R�ϵ��溯��������f��0��=0������Ϊ|f��x1��-f��x2��|��2|x1-x2|����x1=x��x2=0����
|f��x��|��2|x|������f��x���ǡ����н纯������
�ʴ�Ϊ�٢�
���� �������ڴ��������ͣ��ؼ����ڶ��¸���������Լ���Ӧ�ã������ѵ�������ѧ֪ʶת��Ϊ�붨����ص���ʽ����Ҫѧ������ѧ֪ʶ�������Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
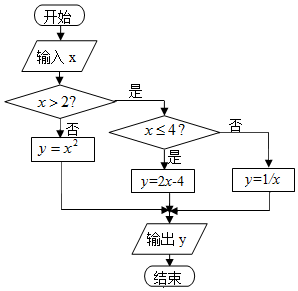 �Ķ������ͼ���ش��������⣺
�Ķ������ͼ���ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\frac{1}{2}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=3x-3 | B�� | y=$\frac{1}{3}$x-$\frac{1}{3}$ | C�� | y=-$\frac{1}{3}$x+$\frac{1}{3}$ | D�� | y=-3x+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com