
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求
,求![]() 零点的个数;
零点的个数;
(3)若![]() 为整数,且当
为整数,且当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
(参考数据![]() ,
, ![]() ,
, ![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)当![]() 时,由
时,由![]() ,且
,且![]() ,即可求解再点
,即可求解再点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,
时, ![]() ,求得
,求得![]() ,从而得到在
,从而得到在![]() ,
, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() 单调递增,确定函数的极值,再根据零点的存在定理,即可得到函数
单调递增,确定函数的极值,再根据零点的存在定理,即可得到函数![]() 有两个不同的零点.
有两个不同的零点.
(3)由题意知, ![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,令
恒成立,令![]() ,得
,得![]() ,从而判定出函数的单调性,进而得到存在
,从而判定出函数的单调性,进而得到存在![]() ,
, ![]() ,即
,即![]() ,得到函数
,得到函数![]() 的最小值
的最小值![]() ,再由
,再由
![]() ,所以
,所以![]() 的取值范围,得出结论.
的取值范围,得出结论.
试题解析:
(1)当![]() 时,
时, ![]() .因为
.因为![]() ,从而
,从而![]() .
.
又![]() ,所以曲线
,所以曲线![]() 在点
在点![]() 处的切线方程
处的切线方程![]() ,
,
即![]() .
.
(2)当![]() 时,
时, ![]() .因为
.因为![]() ,从而,
,从而,
当![]() ,
, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() 有极小值.
有极小值.
因![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 之间有一个零点.
之间有一个零点.
因为![]() ,所以
,所以![]() 在
在![]() 之间有一个零点.
之间有一个零点.
从而![]() 有两个不同的零点.
有两个不同的零点.
(3)由题意知, ![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 为增函数.
为增函数.
因为![]() ,
, ![]() ,
,
所以存在![]() ,
, ![]() ,即
,即![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() 的最小值
的最小值![]() .
.
因为![]() ,所以
,所以![]() .
.
故所求的整数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.
的值;若不存在,请说理由.
(参考数据: ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
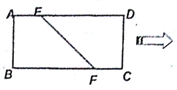
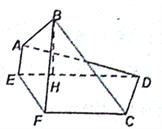
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,离心率
,离心率![]() ,其中一个焦点的坐标为
,其中一个焦点的坐标为![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当点![]() 在椭圆
在椭圆![]() 上运动时,设动点
上运动时,设动点![]() 的运动轨迹为
的运动轨迹为![]() 若点
若点![]() 满足:
满足: ![]() 其中
其中![]() 是
是![]() 上的点.直线
上的点.直线![]() 的斜率之积为
的斜率之积为![]() ,试说明:是否存在两个定点
,试说明:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA-csinC=b(sinA-sinB).
(Ⅰ)求角C的大小;
(Ⅱ)若边长c=4,求△ABC的周长最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com