证明: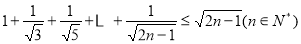 .
.
见解析
【解析】
试题分析:先验证n=1时命题成立,然后假设n=k时成立,再证明n=k+1也成立即可.
①当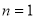 ,不等式显然成立. 2分
,不等式显然成立. 2分
②假设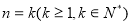 时不等式成立,
时不等式成立,
即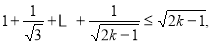 4分
4分
当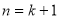 时,
时,
左边=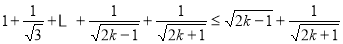
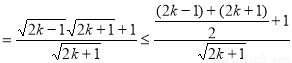
 不等式成立. 7分
不等式成立. 7分
由①②可知,对一切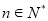 都有
都有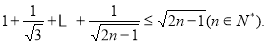 8分
8分
考点:数学归纳法的原理及证明步骤.
练习册系列答案
相关习题
科目:高中数学
来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期中考试理科数学试卷(解析版)
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期中考试理科数学试卷(解析版)
题型:选择题
在复平面内,复数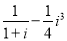 对应的点位于
对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学
来源:2015届甘肃省高二下学期期中考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>
科目:高中数学
来源:2015届湖南省衡阳市上学期高二期末考试文科数学试卷(解析版)
题型:选择题
查看答案和解析>>

 .
. 字词句段篇系列答案
字词句段篇系列答案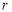 与它的高
与它的高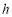 的关系是:
的关系是: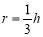 ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径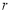 与正四面体高
与正四面体高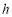 的关系是 .
的关系是 .