
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 与
与![]() 分别沿
分别沿![]() 向上翻折,使
向上翻折,使![]() 重合,则形成的三棱锥的外接球的表面积为_______.
重合,则形成的三棱锥的外接球的表面积为_______.

科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为300元;分4期或5期付款,其利润为400元,![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件![]() :“购买该商品的3位顾客中,至少有1位采用期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用期付款”的概率![]() ;
;
(2)求![]() 的分布列、期望和方差.
的分布列、期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
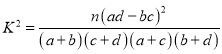 (其中
(其中 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,离心率为
轴,离心率为![]() ,且长轴长是短轴长的
,且长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 过椭圆
过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]()
![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com