
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
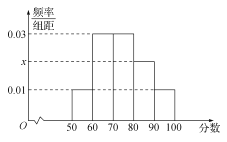
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
【答案】(1)![]() ,平均数是74,中位数是
,平均数是74,中位数是![]() ;(2)1200;(3)
;(2)1200;(3)![]() .
.
【解析】试题分析:(1)根据个矩形面积和为![]() 可得第4组的频率为
可得第4组的频率为![]() ,从而可得结果;(2)由(1)可知,50名学生中成绩不低于70分的频率为
,从而可得结果;(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,从而可得成绩不低于70分的人数;(3)根据分层抽样方法可得这三组中所抽取的人数分别为3,2,1,列举出中任抽取3人的所有可能结果共20种,其中后两组中没有人被抽到的可能结果只有1种,由古典概型概率公式可得结果.
,从而可得成绩不低于70分的人数;(3)根据分层抽样方法可得这三组中所抽取的人数分别为3,2,1,列举出中任抽取3人的所有可能结果共20种,其中后两组中没有人被抽到的可能结果只有1种,由古典概型概率公式可得结果.
(1)由频率分布直方图可得第4组的频率为![]()
![]() ,
,
故![]() .
.
故可估计所抽取的50名学生成绩的平均数为
![]()
![]()
![]() (分).
(分).
由于前两组的频率之和为![]() ,前三组的频率之和为
,前三组的频率之和为![]() ,故中位数在第3组中.
,故中位数在第3组中.
设中位数为![]() 分,
分,
则有![]() ,所以
,所以![]() ,
,
即所求的中位数为![]() 分.
分.
(2)由(1)可知,50名学生中成绩不低于70分的频率为![]() ,
,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为![]() .
.
(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在![]() 这组的3名学生分别为
这组的3名学生分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 这组的2名学生分别为
这组的2名学生分别为![]() ,
,![]() ,成绩在
,成绩在![]() 这组的1名学生为
这组的1名学生为![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共20种.
共20种.
其中后两组中没有人被抽到的可能结果为![]() ,只有1种,
,只有1种,
故后两组中至少有1人被抽到的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足(an+1﹣1)(an﹣1)= ![]() (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn= ![]() .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ![]() ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥ ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱ABC﹣A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC= ![]() ,点O为AC的中点.
,点O为AC的中点. 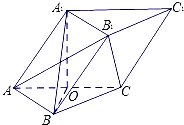
(1)求证:AC⊥平面A1OB;
(2)求二面角B1﹣AC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣lnx﹣1,g(x)=k(f(x)﹣x)+ ![]() ,(k∈R).
,(k∈R).
(1)求曲线y=f(x)在(2,f(2))处的切线方程;
(2)求函数g(x)的单调区间;
(3)当1<k<3,x∈(1,e)时,求证:g(x)>﹣ ![]() (1+ln3).
(1+ln3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点所在直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() x,﹣sin
x,﹣sin ![]() x),且x∈[0,
x),且x∈[0, ![]() ].求:
].求:
(1)![]() 及
及 ![]() ;
;
(2)若f(x)= ![]() ﹣2λ
﹣2λ ![]() 的最小值是﹣
的最小值是﹣ ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com