
2
| ||
| 3 |
(R+1)2-(
|
| 1 |
| 3 |


科目:高中数学 来源: 题型:
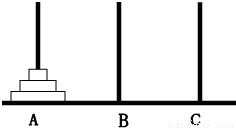
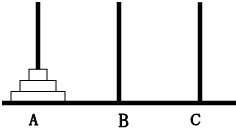 如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是( )
如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是( )查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型:044
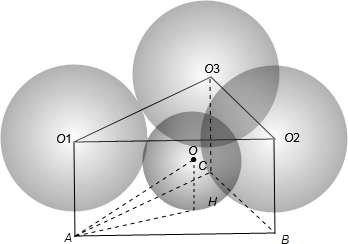
在桌面上有三个球两两相切,且半径都为1,在桌面与三球间放置一个小球,使它与三个球相切.求此小球半径.
查看答案和解析>>
科目:高中数学 来源:2010年福建省高考数学考前指导试卷(文科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省涟源一中、双峰一中高三(下)第五次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com