
(本小题满分12分)在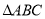 中,
中,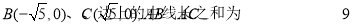 .
.
(Ⅰ)求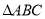 重心G的轨迹方程
重心G的轨迹方程
(Ⅱ)设P为(1)中所求轨迹上任意一点,求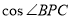 的最小值.
的最小值.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)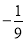 .
.
【解析】
试题分析:(Ⅰ)因为AB、AC边上的中线长为定值9,由重心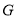 的性质,知
的性质,知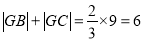 ,即动点G到两定点B、C的距离之和为定值6,且
,即动点G到两定点B、C的距离之和为定值6,且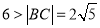 ,所以
,所以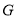 点轨迹符合椭圆轨迹定义,根据椭圆定义相关性质易求得
点轨迹符合椭圆轨迹定义,根据椭圆定义相关性质易求得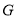 点轨迹方程;(Ⅱ)据已知,点
点轨迹方程;(Ⅱ)据已知,点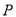 在椭圆上,由椭圆定义可得
在椭圆上,由椭圆定义可得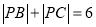 (定值),
(定值),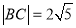 ,由余弦定理可得
,由余弦定理可得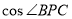 的表达式,结合相关等价变形和基本不等式可得所求.
的表达式,结合相关等价变形和基本不等式可得所求.
试题解析:(Ⅰ)设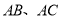 的中点分别为
的中点分别为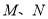 (如下图所示),则据题意
(如下图所示),则据题意
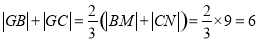 ,即动点G到两定点B、C的距离之和为定值6,
,即动点G到两定点B、C的距离之和为定值6,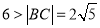 ,
,

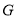 点轨迹为以B、C为焦点的椭圆,
点轨迹为以B、C为焦点的椭圆,
 据题意可设椭圆方程为
据题意可设椭圆方程为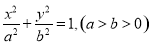 ,则
,则
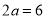 ,
,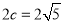 ,即
,即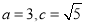 ,根据椭圆的相关性质得
,根据椭圆的相关性质得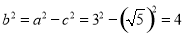 ,
,
所以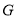 点的轨迹方程为
点的轨迹方程为 ;
;

(Ⅱ)由(Ⅰ)知,点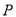 在椭圆上(如上图所示),由椭圆定义可得
在椭圆上(如上图所示),由椭圆定义可得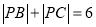 (定值) ,
(定值) , 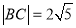 ,由余弦定理可得:
,由余弦定理可得:
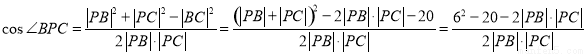
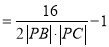 ,显然当
,显然当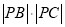 取得最大值时
取得最大值时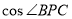 最小,
最小,
根据基本不等式得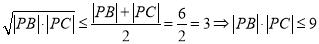 ,即
,即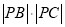 的最大值为9,
的最大值为9,
所以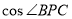 的最小值为
的最小值为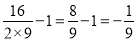 .
.
考点:①椭圆的定义和性质;②椭圆的标准方程;③基本不等式;④最值求解的基本思想.


科目:高中数学 来源:2014-2015学年辽宁省分校高二10月月考数学试卷(解析版) 题型:填空题
在数列{an}中,a1=1,an+1= (n∈N*),则这个数列的通项公式是
(n∈N*),则这个数列的通项公式是 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:选择题
各项均为实数的等比数列{a n }前n项之和记为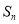 ,若
,若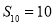 ,
, 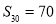 , 则
, 则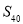 等于
等于
A.150 B.?200 C.150或 ?200 D.?50或400
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com