
 如图,长方体ABCD-A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.
如图,长方体ABCD-A1B1C1D1中,AA1=AD=1,AB=2,点E是C1D1的中点.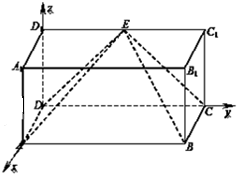
| DE |
| BE |
| BC |
| DE |
| BE |
| DE |
| BC |
| n |
|
| n |
| DE |
| n |
| DE |
| ||||
|
|
| 1 |
| 2 |


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| x |
| 60-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2a2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 命中环数 | 7 | 8 | 9 | 10 |
| 概 率 | 0.12 | 0.18 | 0.28 | 0.32 |
查看答案和解析>>
科目:高中数学 来源: 题型:
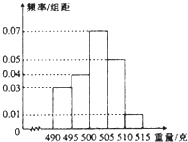 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的N件产品作为样本称出它们的重量(单位;克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示,若其中重量超过510克的产品件数为3.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的N件产品作为样本称出它们的重量(单位;克),重量的分组区间为(490,495],(495,500],…(510,515],由此得到样本的频率分布直方图,如图所示,若其中重量超过510克的产品件数为3.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com