解:(Ⅰ)设C(m,0),D(0,n),P(x,y).
由
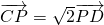
,得(x-m,y)=

(-x,n-y),
∴x-m=-

x,y=

(n-y),
由|CD|=

+1,得m
2+n
2=(

+1)
2,
∴(

+1)
2x
2+
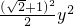
=(

+1)
2,
整理,得曲线E的方程为x
2+

=1
(II)设A(x
1,y
1),B(x
2,y
2),
由

知点M坐标为(x
1+x
2,y
1+y
2).
设直线l的方程为y=kx+1,代入曲线E方程,得(k
2+2)x
2+2kx-1=0,
则x
1+x
2=-
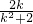
,x
1x
2=-
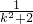
,
y
1+y
2=k(x
1+x
2)+2=
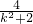
,
由点M在曲线E上,知(x
1+x
2)
2+

=1,
即(-
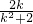
)
2+
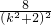
=1
解得k
2=2.
∴x
1x
2+y
1y
2=(1+k
2)x
1x
2+k(
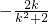
)+1=-

∴

=-

.
分析:(Ⅰ)设C、D、P的坐标,利用
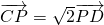
,确定坐标之间的关系,由|CD|=

+1,得m
2+n
2=(

+1)
2,从而可得曲线E的方程;
(II)设A(x
1,y
1),B(x
2,y
2),由

知点M坐标为(x
1+x
2,y
1+y
2).设直线l的方程为y=kx+1,代入曲线E方程,利用韦达定理及点M在曲线E上,求得k
2=2,再利用向量的数量积公式,即可求得结论.
点评:本题考查向量知识的运用,考查轨迹方程,考查直线与曲线的位置关系,正确运用向量,确定坐标之间的关系是关键.

 的线段的两端点C、D分别在x轴、y轴上滑动,
的线段的两端点C、D分别在x轴、y轴上滑动,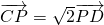 .记点P的轨迹为曲线E.
.记点P的轨迹为曲线E. ,当点M在曲线E上时,求
,当点M在曲线E上时,求 的值.
的值.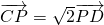 ,得(x-m,y)=
,得(x-m,y)= (-x,n-y),
(-x,n-y), x,y=
x,y= (n-y),
(n-y), +1,得m2+n2=(
+1,得m2+n2=( +1)2,
+1)2, +1)2x2+
+1)2x2+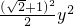 =(
=( +1)2,
+1)2, =1
=1 知点M坐标为(x1+x2,y1+y2).
知点M坐标为(x1+x2,y1+y2).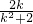 ,x1x2=-
,x1x2=-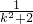 ,
,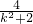 ,
, =1,
=1,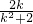 )2+
)2+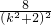 =1
=1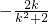 )+1=-
)+1=-
 =-
=- .
.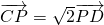 ,确定坐标之间的关系,由|CD|=
,确定坐标之间的关系,由|CD|= +1,得m2+n2=(
+1,得m2+n2=( +1)2,从而可得曲线E的方程;
+1)2,从而可得曲线E的方程; 知点M坐标为(x1+x2,y1+y2).设直线l的方程为y=kx+1,代入曲线E方程,利用韦达定理及点M在曲线E上,求得k2=2,再利用向量的数量积公式,即可求得结论.
知点M坐标为(x1+x2,y1+y2).设直线l的方程为y=kx+1,代入曲线E方程,利用韦达定理及点M在曲线E上,求得k2=2,再利用向量的数量积公式,即可求得结论.

 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2