
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断![]() 在定义域上的单调性并加以证明;
在定义域上的单调性并加以证明;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 恒成立, 求
恒成立, 求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知y=f(x)为二次函数,若y=f(x)在x=2处取得最小值﹣4,且y=f(x)的图象经过原点,
(1)求f(x)的表达式;
(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,且AC=BD,平面PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)在△PAD中,AP=2,AD=2 ![]() ,PD=4,三棱锥E﹣ACD的体积是
,PD=4,三棱锥E﹣ACD的体积是 ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() 和椭圆
和椭圆![]() 的焦点相同且
的焦点相同且![]() .给出如下四个结论:
.给出如下四个结论:
①椭圆![]() 与椭圆
与椭圆![]() 一定没有公共点 ②
一定没有公共点 ②![]()
③![]() ④
④![]()
其中所有正确结论的序号是( )
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
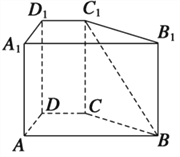
【题目】如图,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求线段BC1的长度;
(Ⅱ)异面直线BC1与DC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线f(x)=ke﹣2x在点x=0处的切线与直线x﹣y﹣1=0垂直,若x1 , x2是函数g(x)=f(x)﹣|1nx|的两个零点,则( )
A.1<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1![]()
C.2<x1x2<2 ![]()
D.![]() <x1x2<2
<x1x2<2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A. 30° B. 45° C. 90° D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com