
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),将Q的坐标代入,结合椭圆的离心率公式及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(2)由题意可知,直线l的斜率存在且不为0,故可设直线n的方程为y=kx+m,A(x1,y1),B(x2,y2),联立椭圆方程,消去y,运用韦达定理和判别式大于0,由等差数列的中项性质,化简整理可得m=0,将直线y=kx代入椭圆方程,求得A,B的坐标和弦长,求得M到直线AB的距离,运用三角形的面积公式可得S△ABM的面积;
(3)令f(k)=$\frac{4(k-1)^{2}}{1+4{k}^{2}}$,求出导数和单调区间,可得S△ABM的面积的平方的最大值,即可得到所求最大值.
解答 解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由点$Q(\sqrt{2},\frac{{\sqrt{2}}}{2})$在椭圆C上,知$\frac{2}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1 ①
又e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$ ②
联立①②解得,a=2,b=1,
所以椭圆方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线n的方程为y=kx+m,A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
消去y得(1+4k2)x2+8kmx+4(m2-1)=0.
△=64k2m2-16(1+4k2)(m2-1)=16(4k2-m2+1)>0,
且x1+x2=-$\frac{8km}{1+4{k}^{2}}$,
因为直线OA,AB,OB的斜率依次成等差数列,
所以$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$=2k,即
x1y2+x2y1=2kx1x2,
又y=kx+m,所以kx1x2+mx2+kx1x2+mx1=2kx1x2,
即为m(x1+x2)=0,即m=0,
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$易得A($\frac{2}{\sqrt{1+4{k}^{2}}}$,$\frac{2k}{\sqrt{1+4{k}^{2}}}$),B(-$\frac{2}{\sqrt{1+4{k}^{2}}}$,-$\frac{2k}{\sqrt{1+4{k}^{2}}}$),
弦AB的长为$\frac{4\sqrt{1+{k}^{2}}}{\sqrt{1+4{k}^{2}}}$,
又点M到直线y=kx的距离d=$\frac{|k-1|}{\sqrt{1+{k}^{2}}}$,
所以S△ABM=$\frac{1}{2}$•$\frac{4\sqrt{1+{k}^{2}}}{\sqrt{1+4{k}^{2}}}$•$\frac{|k-1|}{\sqrt{1+{k}^{2}}}$=$\frac{2|k-1|}{\sqrt{1+4{k}^{2}}}$;
(3)令f(k)=$\frac{4(k-1)^{2}}{1+4{k}^{2}}$,则f′(k)=$\frac{8(k-1)(4k+1)}{(1+4{k}^{2})^{2}}$,
易知f(k)在(-∞,-$\frac{1}{4}$),(1,+∞)上单调递增,在(-$\frac{1}{4}$,1)上单调递减.
又f(-$\frac{1}{4}$)=5,且x→+∞时,f(k)→1.
所以当k=-$\frac{1}{4}$时,f(k)取最大值5,
此时,S△ABM的面积取最大值$\sqrt{5}$.
点评 本题考查椭圆的方程和性质,主要是离心率,考查直线和椭圆方程联立,运用韦达定理,同时考查等差数列中项的性质,以及直线的斜率公式,点到直线的距离公式,三角形的面积的最值的求法,注意运用导数,判断单调性,考查化简整理的运算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
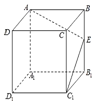 如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )| A. | 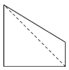 | B. | 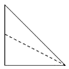 | C. | 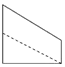 | D. | 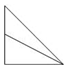 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com