
分析 (1)当a=-1时,命题$p:?n∈{N}^{*},{(-1)}^{n+1}<2+\frac{{(-1)}^{n+1}}{n}$,即$(1-\frac{1}{n}{)(-1)}^{n+1}<2$,可判断其真假;
命题q:当$?x∈(0,\frac{π}{2}),(sinx+1)(cosx+1)=1$,即$?x∈(0,\frac{π}{2})$,sinx+cosx=-sinxcosx,可判断其真假;
(2)如果p∧q为假命题,p∨q为真命题,则命题p,q一真一假,进而得到实数a的取值范围.
解答 解:(1)当a=-1时,
命题$p:?n∈{N}^{*},{(-1)}^{n+1}<2+\frac{{(-1)}^{n+1}}{n}$,
即$(1-\frac{1}{n}{)(-1)}^{n+1}<2$恒成立,
故命题p为真命题;
命题q:当$?x∈(0,\frac{π}{2}),(sinx+1)(cosx+1)=1$,
即$?x∈(0,\frac{π}{2})$,sinx+cosx=-sinxcosx,
由sinx+cosx>0,-sinxcosx<0得:命题q为假命题,
(2)若命题$p:?n∈{N^*},{({-1})^n}•({2a+1})<2+\frac{{{{({-1})}^{n+1}}}}{n}$为真,
即$\left\{\begin{array}{l}2a+1>-2-\frac{1}{n},n为奇数\\ 2a+1<2-\frac{1}{n},n为偶数\end{array}\right.$恒成立,
即$\left\{\begin{array}{l}2a>-3-\frac{1}{n},n为奇数\\ 2a<1-\frac{1}{n},n为偶数\end{array}\right.$恒成立,
即$\left\{\begin{array}{l}2a≥-3\\ 2a<\frac{1}{2}\end{array}\right.$,
解得:a∈$[-\frac{3}{2},\frac{1}{4})$,
若命题q:当$?x∈({0,\frac{π}{2}}),({sinx-a})({cosx-a})={a^2}$为真,
即sinx+cosx=asinxcosx,
即a=$\frac{sinxcosx}{sinx+cosx}$,
令t=sinx+cosx,t∈(1,$\sqrt{2}$],
则a=$\frac{1}{2}$(t-$\frac{1}{t}$)∈(0,$\frac{\sqrt{2}}{4}$],
如果p∧q为假命题,p∨q为真命题,
则命题p,q一真一假;
当p真q假时,a∈$[-\frac{3}{2},0]$,
当p假q真时,a∈$[\frac{1}{4},\frac{\sqrt{2}}{4}]$,
综上可得:a∈$[-\frac{3}{2},0]$∪$[\frac{1}{4},\frac{\sqrt{2}}{4}]$.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,特称命题的否定,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
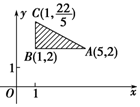 如图所示的坐标平面的可行域内(包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,±3) | B. | (±3,0) | C. | (±1,0) | D. | (0,±1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
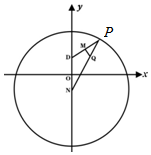 如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.
如图,已知圆N:x2+(y+$\sqrt{5}$)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,$\sqrt{5}$)和DP上的点M,满足$\overrightarrow{DP}$=2$\overrightarrow{DM}$,$\overrightarrow{MQ}$•$\overrightarrow{DP}$=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com