
(本小题共13分) 已知圆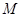 过两点
过两点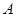 (1,-1),
(1,-1),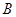 (-1,1),且圆心
(-1,1),且圆心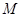 在
在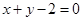 上.
上.
(1)求圆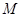 的方程;
的方程;
(2)设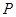 是直线
是直线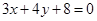 上的动点,
上的动点,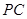 、
、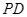 是圆
是圆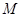 的两条切线,
的两条切线,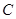 、
、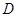 为切点,求四边形
为切点,求四边形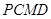 面积的最小值.
面积的最小值.
(1)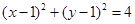 (2)
(2)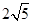
【解析】
试题分析:(1)法一:
线段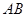 的中点为(0,0),其垂直平分线方程为
的中点为(0,0),其垂直平分线方程为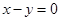 .
…2分
.
…2分
解方程组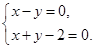 所以圆
所以圆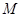 的圆心坐标为(1,1).
…4分
的圆心坐标为(1,1).
…4分
故所求圆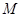 的方程为:
的方程为: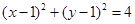 . … 6分
. … 6分
法二:设圆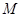 的方程为:
的方程为: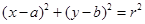 ,
,
根据题意得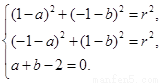 … 2分
… 2分
解得 .
… 4分
.
… 4分
故所求圆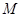 的方程为:
的方程为: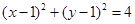 .
… 6分
.
… 6分
(2)由题知,四边形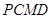 的面积为
的面积为
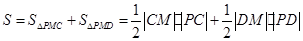 . … 8分
. … 8分
又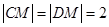 ,
,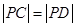 ,
,
所以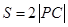 ,而
,而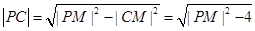 ,
… 10分
,
… 10分
即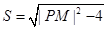 .
… 11分
.
… 11分
因此要求 的最小值,只需求
的最小值,只需求 的最小值即可,
的最小值即可,
即在直线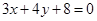 上找一点
上找一点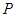 ,使得
,使得 的值最小,
的值最小,
所以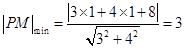 ,
… 12分
,
… 12分
所以四边形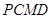 面积的最小值为
面积的最小值为
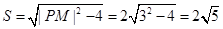 .
… 13分
.
… 13分
考点:本小题主要考查圆的标准方程的求法、直线与圆的位置关系的判断和应用,考查学生分析问题、解决问题的能力和运算求解能力.
点评:求解直线与圆的位置关系时,要注意数形结合,可以简化运算,还要注意适当转化.直线和圆所涉及到的知识是整个解析几何的基础,并渗透到解析几何的各个部分,但一般难度不大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本小题共13分)
已知函数![]()
(I)若x=1为![]() 的极值点,求a的值;
的极值点,求a的值;
(II)若![]() 的图象在点(1,
的图象在点(1,![]() )处的切线方程为
)处的切线方程为![]() ,
,
(i)求![]() 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(ii)求函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三压轴文科数学试卷(解析版) 题型:解答题
(本小题共13分)
已知向量 ,设函数
,设函数 .
.
(Ⅰ)求函数 在
在 上的单调递增区间;
上的单调递增区间;
(Ⅱ)在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, 的面积为
的面积为 ,求边
,求边 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市丰台区高三下学期统一练习数学理卷 题型:解答题
(本小题共13分)
某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
(Ⅰ)求分别获得一、二、三等奖的概率;
(Ⅱ)设摸球次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:北京市宣武区2010年高三第一次质量检测数学(文)试题 题型:解答题
(本小题共13分)
已知函数
(I)当a=1时,求函数 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;
(II)当a=2时,在 的条件下,求
的条件下,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com