
(本小题满分12分)
已知圆C: .
.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P( )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
(1) y=(2±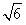 )x. (2)
)x. (2)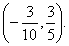
解析试题分析:解(1)将圆C配方得 .
.
① 当直线在两坐标轴上的截距为零时,设直线方程为y=kx,由直线与圆相切得 ,
,
即k=2±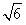 ,从而切线方程为y=(2±
,从而切线方程为y=(2±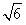 )x.
)x.
②当直线在两坐标轴上的截距不为零时,设直线方程为x+y-a=0,由直线与圆相切得x+y+1=0或x+y-3=0.
(2)由|PO|=|PM|得 得
得  .
.
即点P在直线l:2x-4y+3=0上,当|PM|取最小值时即|OP|取得最小值,直线OP⊥l,
∴直线OP的方程为2x+y=0. 解方程组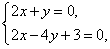 得P点坐标为
得P点坐标为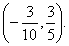
考点:本试题考查了圆的知识。
点评:对于解决圆的切线问题,一般要利用圆心到直线的距离等于圆的半径来分析,同时要对于截距的理解,注意截距都为零的情况容易丢解。同时对于距离 相等,结合切线长定理来分析最值,属于中档题。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
己知圆 直线
直线 .
.
(1) 求与圆 相切, 且与直线
相切, 且与直线 平行的直线
平行的直线 的方程;
的方程;
(2) 若直线 与圆
与圆 有公共点,且与直线
有公共点,且与直线 垂直,求直线
垂直,求直线 在
在 轴上的截距
轴上的截距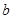 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知关于 的方程
的方程 :
: .
.
(1)当 为何值时,方程C表示圆。
为何值时,方程C表示圆。
(2)若圆C与直线 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= ,求
,求 的值。
的值。
(3)在(2)条件下,是否存在直线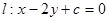 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为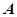 ,过点
,过点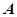 与
与 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过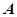 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,求椭圆
相切,求椭圆 的
的
方程;
(3)在(2)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于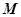 、
、 两
两
点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,
为邻边的平行四边形是菱形,
如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com