
(本题17分)已知定义在 上的函数
上的函数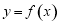 是偶函数,且
是偶函数,且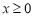 时,
时, ,(1)当
,(1)当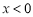 时,求
时,求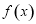 解析式;(2)写出
解析式;(2)写出 的单调递增区间.
的单调递增区间.
(1)当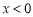 时,
时, ;(2)
;(2) 的单调递增区间是
的单调递增区间是 和
和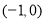 .
.
【解析】
试题分析:(1)任取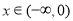 ,则
,则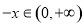 ,由
,由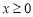 时,
时,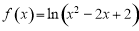 ,得出
,得出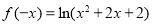 ;利用
;利用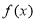 是偶函数,知
是偶函数,知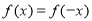 ,进而求得
,进而求得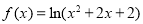 ;
;
(2).因为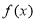 是偶函数,所以只需求出函数
是偶函数,所以只需求出函数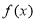 在
在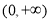 上的单调性,然后根据函数奇偶性与单调性的关系,求出函数
上的单调性,然后根据函数奇偶性与单调性的关系,求出函数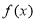 在
在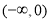 上的单调性,进而求得函数
上的单调性,进而求得函数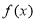 在
在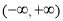 上的单调性;在判断函数
上的单调性;在判断函数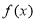 在
在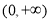 上的单调性时,可以用复合函数的单调性,也可以用单调性的定义,也可以用导数;本题是用复合函数的单调性解答的.
上的单调性时,可以用复合函数的单调性,也可以用单调性的定义,也可以用导数;本题是用复合函数的单调性解答的.
试题解析:(1)任取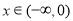 ,则
,则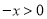 , 2分
, 2分
∵当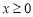 时,
时,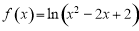 ,∴
,∴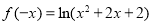 , 4分
, 4分
∵函数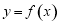 是定义在
是定义在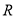 上的偶函数,∴
上的偶函数,∴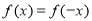 ,
,
∴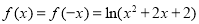 ,∴当
,∴当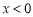 时,
时, ; 7分
; 7分
(2)当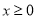 时,
时,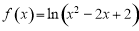 ,此时,令
,此时,令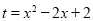 ,
,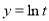 , 9分
, 9分
则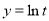 在
在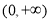 上是增函数;
上是增函数;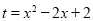 在
在 上是减函数,在
上是减函数,在 上是增函数,且
上是增函数,且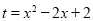 的值域为
的值域为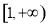 ; 11分
; 11分
由复合函数单调性知,当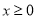 时,
时,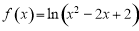 的单调递增区间是
的单调递增区间是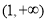 ,单调递减区间是
,单调递减区间是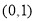 ;
;
∴当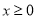 时,函数
时,函数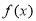 的单调递增区间是
的单调递增区间是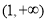 ,单调递减区间是
,单调递减区间是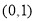 ; 13分
; 13分
又∵函数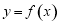 是定义在
是定义在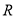 上的偶函数,
上的偶函数,
∴当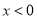 时,函数
时,函数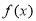 的单调递增区间是
的单调递增区间是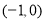 ,单调递减区间是
,单调递减区间是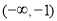 ; 15分
; 15分
综上可知,函数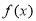 的单调递增区间是
的单调递增区间是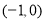 和
和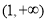 . 17分
. 17分
考点:①函数的奇偶性;②函数及复合函数的单调性;③利用函数的奇偶性求解析式;④函数奇偶性与单调性的关系.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2014-2015学年河南省郑州市高二10月月考数学试卷(解析版) 题型:填空题
我国西部一个地区的年降水量在下列区间内的概率如下表所示:
年降水量/mm | [ 100, 150 ) | [ 150, 200 ) | [ 200, 250 ) | [ 250, 300 ] |
概率 | 0.21 | 0.16 | 0.13 | 0. 12 |
则年降水量在 [ 200,300 ] (mm)范围内的概率是___________
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:解答题
已知数列 的前
的前 项和
项和 ,且
,且 。
。
(1)求数列 的通项公式;
的通项公式;
(2)令 ,是否存在
,是否存在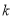 (
( ),使得
),使得 成等比数列。若存在,求出所有符合条件的
成等比数列。若存在,求出所有符合条件的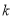 值;若不存在,请说明理由。
值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:选择题
如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛.顶层一个,以下各层堆成正六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共有 13个花盆,则底层的花盆的个数是( )

A.91 B.127 C.169 D.255
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
B.命题“?x0∈R,x02+x0-1<0”的否定是“?x∈R,x2+x-1>0”
C.命题“若x=y,则sin x=sin y”的逆否命题为假命题
D.若“p或q”为真命题,则p,q中至少有一个为真命题
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:填空题
抛掷一个骰子,若掷出5点或6点就说试验成功,则在3次试验中恰有2次成功的概率为__________。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二10月月考数学试卷(解析版) 题型:解答题
数列 满足
满足
(1)证明:数列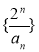 是等差数列;
是等差数列;
(2)求数列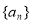 的通项公式
的通项公式 ;
;
(3)设 ,求数列
,求数列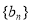 的前
的前 项和
项和 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com