
【题目】已知曲线C:x2+y2-2x-4y+m=0
(1)当m为何值时,曲线C表示圆;
(2)若曲线C与直线x+2y-4=0交于M、N两点,且OM⊥ON(O为坐标原点),求m的值。
【答案】(1)m<5;(2)m=![]() .
.
【解析】试题分析:(1)由二元二次方程表示圆的条件D2+E2-4F大于0列出关于m的不等式,求出不等式的解集即可得到m的取值范围;(2)设出曲线与直线的交点M和N的坐标,联立曲线C与直线的方程,消去y后得到关于x的一元二次方程,利用韦达定理表示出两根之和与两根之积,然后由OM与ON垂直得到M和N横坐标之积与纵坐标之积的和为0,由直线方程化为横坐标的关系式,把表示出的两根之和与两根之积代入即可求出m的值.
试题解析:
(1)由D2+E2-4F=4+16-4m=20-4m>0,得m<5
(2)设M(x1,y1),N(x2,y2),由OM⊥ON得x1x2+ y1y2=0.
将直线方程x+2y-4=0与曲线C:x2+y2-2x-4y+m=0联立并消去y得
5x2-8x+4m-16=0,由韦达定理得x1+x2=![]() ①,x1x2=
①,x1x2=![]() ②,
②,
![]() =64-20(4m-16)=384-80m﹥0﹥所以m﹤4
=64-20(4m-16)=384-80m﹥0﹥所以m﹤4![]()
又由x+2y-4=0得y=![]() (4-x),
(4-x),
∴x1x2+y1y2=x1x2+![]() (4-x1)·
(4-x1)·![]() (4-x2)=
(4-x2)= ![]() x1x2-( x1+x2)+4=0.
x1x2-( x1+x2)+4=0.
将①、②代入得m=![]() ,满足
,满足![]() ﹥ 0.
﹥ 0.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|﹣|x+1|.
(1)求不等式|f(x)|<1的解集;
(2)若不等式|a|f(x)≥|f(a)|对任意a∈R恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,给出下列四个命题: ①若|z1﹣z2|=0,则 ![]() =
= ![]() ②若z1=
②若z1= ![]() ,则
,则 ![]() =z2
=z2
③若|z1|=|z2|,则z1 ![]() =z2
=z2 ![]() ④若|z1|=|z2|,则z12=z22
④若|z1|=|z2|,则z12=z22
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
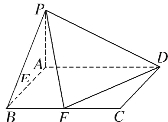
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.
(1)证明:![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,若存在,确定点
,若存在,确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(3)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的一系列对应值如表:
)的一系列对应值如表:

(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果:
①当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com