
【题目】在数列{an}中, ![]() ,
, ![]() ,
, ![]() ,其中n∈N* .
,其中n∈N* .
(1)求证:数列{bn}为等差数列;
(2)设cn=bnbn+1cosnπ,n∈N* , 数列{cn}的前n项和为Tn , 若当n∈N*且n为偶数时, ![]() 恒成立,求实数t的取值范围;
恒成立,求实数t的取值范围;
(3)设数列{an}的前n项的和为Sn , 试求数列{S2n﹣Sn}的最大值.
【答案】
(1)证明:∵ 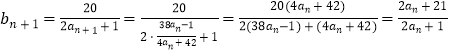 ,
,
∴ ![]() ,
,
∴数列{bn}是公差为1的等差数列
(2)解:由(1)可知, ![]() ,故bn=n.
,故bn=n.
因为 ![]() ,
,
所以Tn=c1+c2+…+cn= ![]() ,
,
当n∈N*且n为偶数时,设n=2m,m∈N*,
则 ![]() =b2(﹣b1+b3)+b4(﹣b3+b5)+…+b2m(﹣b2m﹣1+b2m+1)=2(b2+b4+…+b2m)=4(1+2+…+m)=
=b2(﹣b1+b3)+b4(﹣b3+b5)+…+b2m(﹣b2m﹣1+b2m+1)=2(b2+b4+…+b2m)=4(1+2+…+m)= ![]() ,
,
要使 ![]() 对n∈N*且n为偶数恒成立,
对n∈N*且n为偶数恒成立,
只要使 ![]() 对n∈N*且n为偶数恒成立,
对n∈N*且n为偶数恒成立,
即使 ![]() 对n为正偶数恒成立,∵
对n为正偶数恒成立,∵ ![]() ,
,
∴t≥1,故实数t的取值范围是[1,+∞)
(3)解:由(1)得 ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
设 ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴当n=1时, ![]() ,即M1<M2,
,即M1<M2,
当n≥2时,Mn+1﹣Mn<0,即M2>M3>M4>…,∴ ![]() ,
,
因此数列{S2n﹣Sn}的最大值为 ![]()
【解析】(1)根据题意,由数列的递推关系式得出bn+1与an的关系式,由等差数列的定义分析可得答案,(2)根据题意求出数列{cn}的前n项和为Tn的表达式,当n∈N*且n为偶数时,设n=2m,m∈N*,求出Tn的表达式,分析可得答案,(3)由(2)的结论求出S2n、Sn,即可得{S2n﹣Sn}的表达式,设M n = S 2 n S n,分析不难得出答案.
【考点精析】通过灵活运用数列的通项公式,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线 ![]() (a为参数),直线l:x﹣y﹣6=0.
(a为参数),直线l:x﹣y﹣6=0.
(1)在曲线C上求一点P,使点P到直线l的距离最大,并求出此最大值;
(2)过点M(﹣1,0)且与直线l平行的直线l1交C于A,B两点,求点M到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() +t
+t ![]() (t为实数).
(t为实数).
(1)若 ![]() ,求当|
,求当| ![]() |取最小值时实数t的值;
|取最小值时实数t的值;
(2)若 ![]() ⊥
⊥ ![]() ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量 ![]() ﹣
﹣ ![]() 和向量
和向量 ![]() 的夹角为
的夹角为 ![]() ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.
(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面半径;
(2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,点列Pn(n=1,2,…)在△ABC内部,且△PnAB与△PnAC的面积比为2:1,若对n∈N*都存在数列{bn}满足 ![]() ,则a4的值为 .
,则a4的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线y=ax+2与曲线y=f(x)交于A、B两点,其中A是切点,记h(x)= ![]() ,g(x)=f(x)﹣ax,则下列判断正确的是( )
,g(x)=f(x)﹣ax,则下列判断正确的是( )
A.h(x)只有一个极值点
B.h(x)有两个极值点,且极小值点小于极大值点
C.g(x)的极小值点小于极大值点,且极小值为﹣2
D.g(x)的极小值点大于极大值点,且极大值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
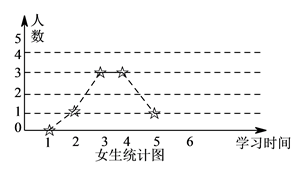
(I)已知该校有 ![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足 ![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于 ![]() 小时的学生中选取
小时的学生中选取 ![]() 人,设选到的男生人数为
人,设选到的男生人数为 ![]() ,求随机变量
,求随机变量 ![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差 ![]() 与女生学习时间方差
与女生学习时间方差 ![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com