
分析 利用等差数列与等比数列的通项公式分别求出{an}以及{bn}和{${\frac{a_n}{b_n}}\right.$}的通项公式,利用错位相减法进行求和,利用不等式恒成立进行求解即可.
解答 解:设数列{an}的公差为d,数列{bn}的公比为q,
由b2+S2=10,a5-2b2=a3.
得$\left\{\begin{array}{l}q+6+d=10\\ 3+4d-2q=3+2d\end{array}\right.$,解得$\left\{\begin{array}{l}d=2\\ q=2\end{array}\right.$
∴an=3+2(n-1)=2n+1,${b_n}={2^{n-1}}$.
则${\frac{a_n}{b_n}}\right.$=$\frac{2n+1}{{2}^{n-1}}$,
Tn=3+$\frac{5}{2}$+$\frac{7}{{2}^{2}}$+…+$\frac{2n+1}{{2}^{n-1}}$,
所以$\frac{1}{2}$Tn=$\frac{3}{2}$+$\frac{5}{{2}^{2}}$+$\frac{7}{{2}^{3}}$+…+$\frac{2n}{{2}^{n-1}}$+$\frac{2n+1}{{2}^{n}}$,
两式作差得$\frac{1}{2}$Tn=3+$\frac{2}{2}$+$\frac{2}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+$\frac{2}{{2}^{4}}$+…+$\frac{2}{{2}^{n-1}}$-$\frac{2n+1}{{2}^{n}}$
=3+(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-2}}$)-$\frac{2n+1}{{2}^{n}}$=3+$\frac{1-(\frac{1}{2})^{n-1}}{1-\frac{1}{2}}$-$\frac{2n+1}{{2}^{n}}$=3+2-2•($\frac{1}{2}$)n-1-$\frac{2n+1}{{2}^{n}}$,
即Tn=10-($\frac{1}{2}$)n-3-$\frac{2n+1}{{2}^{n-1}}$<10,
由Tn<M对一切正整数n都成立,
∴M≥10,
故M的最小值为10,
故答案为:10
点评 本题主要考查数列通项公式的求解以及数列求和的计算,利用错位相减法是解决本题的关键.考查学生的计算能力.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
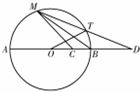 如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.
如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [0,1] | C. | [1,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | 8 |
| 不肥胖 | 4 | 18 | 22 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
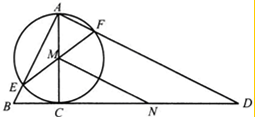 AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8
AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com