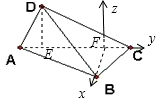
解:如图,过点D、B分别向AC引垂线,垂足分别为E、F,则AE=CF=1,EF=3,DE=BF=2.
因为DE⊥AC,面ACD∩面ABC=AC,二面角D-AC-B为直二面角,所以DE⊥平面ABC,
又因为BF?平面ABC,所以DE⊥BF,故DE、AC、BF两两垂直.
如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
则各点的坐标如下A(0,-4,0),B(2,0,0),C(0,1,0),D(0,-3,2).(3分)
(Ⅰ)

=(0,1,2),

=(2,4,0),

=(-2,1,0),

=(0,-4,2)
设平面ABD的法向量为

=(x,y,1),则
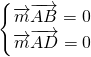
,∴
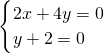
,∴
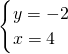
,
即

=(4,-2,1)
设平面BCD的法向量为

=(1,b,c),则
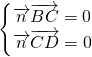
,

,∴
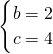
即

=(1,2,4)
∴cos<

,

>=

=
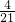
.
由图形知二面角A-BD-C平面角的余弦值为-
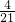
.(8分)
(Ⅱ)设O为AC的中点,∵△ABC与△ADC都为直角三角形,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心.
∴四面体ABCD的体积
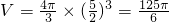
(12分)
分析:(Ⅰ)过点D、B分别向AC引垂线,垂足分别为E、F,可证DE、AC、BF两两垂直.以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系,用坐标表示点与向量,确定平面ABD的法向量

=(4,-2,1),平面BCD的法向量

=(1,2,4),利用向量的夹角公式,即可求得结论;
(Ⅱ)设O为AC的中点,可得O为四面体ABCD的外接球的球心,从而可求四面体ABCD的体积.
点评:本题考查面面角,考查四面体体积的计算,考查利用空间向量解决空间角问题,属于中档题.

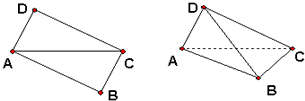 如图,矩形ABCD中,AB=CD=2
如图,矩形ABCD中,AB=CD=2 ,BC=AD=
,BC=AD= .现沿着其对角线AC将D点向上翻折,使得二面角D-AC-B为直二面角.
.现沿着其对角线AC将D点向上翻折,使得二面角D-AC-B为直二面角. 解:如图,过点D、B分别向AC引垂线,垂足分别为E、F,则AE=CF=1,EF=3,DE=BF=2.
解:如图,过点D、B分别向AC引垂线,垂足分别为E、F,则AE=CF=1,EF=3,DE=BF=2. =(0,1,2),
=(0,1,2), =(2,4,0),
=(2,4,0), =(-2,1,0),
=(-2,1,0), =(0,-4,2)
=(0,-4,2) =(x,y,1),则
=(x,y,1),则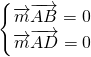 ,∴
,∴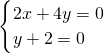 ,∴
,∴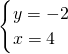 ,
, =(4,-2,1)
=(4,-2,1) =(1,b,c),则
=(1,b,c),则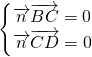 ,
, ,∴
,∴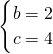
 =(1,2,4)
=(1,2,4) ,
, >=
>= =
=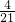 .
.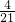 .(8分)
.(8分)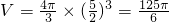 (12分)
(12分) =(4,-2,1),平面BCD的法向量
=(4,-2,1),平面BCD的法向量 =(1,2,4),利用向量的夹角公式,即可求得结论;
=(1,2,4),利用向量的夹角公式,即可求得结论;

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB= A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,DC=
如图,矩形ABCD中,DC= (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD