
【题目】在平面直角坐标系![]() 内,有一动点
内,有一动点![]() 到直线
到直线![]() 的距离和到点
的距离和到点![]() 的距离比值是
的距离比值是![]()
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() (异于点
(异于点![]() )为曲线
)为曲线![]() 上一个动点,过点
上一个动点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交曲线
交曲线![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)直接根据题意设点,列式,化简,即可求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)先考虑特殊情况,当直线![]() 的斜率为
的斜率为![]() 时,可计算出
时,可计算出![]() ,再考虑一般情况,
,再考虑一般情况,
当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 的方程联立求出点
的方程联立求出点![]() 的坐标得出
的坐标得出![]() 的长,同理,将直线
的长,同理,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立求出
的方程联立求出![]() ,继而得到
,继而得到![]() 的表达式,最后根据函数知识即可求出
的表达式,最后根据函数知识即可求出![]() 的最小值.
的最小值.
(1)设动点![]() 的坐标为
的坐标为![]() ,根据题意得
,根据题意得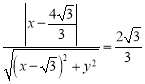 ,再考虑一般情况,当
,再考虑一般情况,当
化简得曲线![]() 的方程为:
的方程为:![]() .
.
(2)当直线![]() 的斜率为
的斜率为![]() 时,
时,![]() 为椭圆
为椭圆![]() 的短轴,则
的短轴,则![]() .
.
所以![]()
当直线![]() 的斜率不为
的斜率不为![]() 时,设直线
时,设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由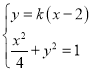 得
得![]() .
.
设![]() 所以
所以![]() ,
,![]()
故![]() ,得
,得![]()
设![]() ,由椭圆对称性可知
,由椭圆对称性可知![]() .
.
由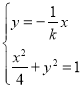 解得
解得![]()
![]() ,所以
,所以![]()
所以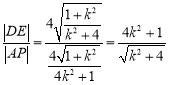
设![]() ,则
,则![]()
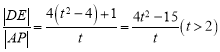 ,令
,令![]() ,则
,则![]()
所以![]() 是一个增函数,所以
是一个增函数,所以![]()
综上,![]() 的最小值是
的最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是坐标原点,椭圆
是坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,若
在椭圆上,若![]() 的面积最大时
的面积最大时![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,点
,点![]() 是第四象限的点且在椭圆
是第四象限的点且在椭圆![]() 上,线段
上,线段![]() 被直线
被直线![]() 垂直平分,直线
垂直平分,直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程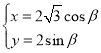 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程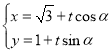 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2018年1月至12月石油进口量统计图(其中同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比),则下列说法错误的是( )
个月之比),则下列说法错误的是( )
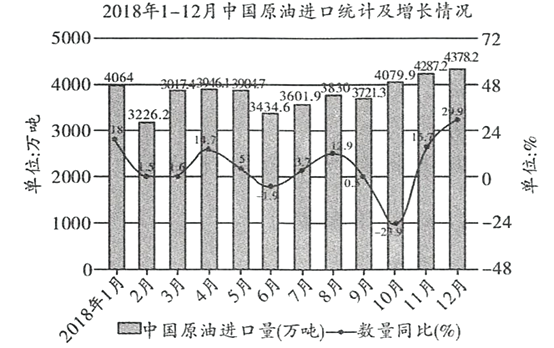
A.2018年下半年我国原油进口总量高于2018年上半年
B.2018年12个月中我国原油月最高进口量比月最低进口量高1152万吨
C.2018年我国原油进口总量高于2017年我国原油进口总量
D.2018年1月—5月各月与2017年同期相比较,我国原油进口量有增有减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足不出户,手机下单,送菜到家,轻松逛起手机“菜市场”,拎起手机“菜篮子”.在省时省心的同时,线上买菜也面临着质量不佳、物流滞后等问题.“指尖”上的菜篮子该如何守护“舌尖”上的幸福感?某手机APP(应用程序)公司为了解这款APP使用者的满意度,对一小区居民开展“线上购买食品满意度调查”活动,邀请每位使用者填写一份满意度测评表(满分100分).该公司最后共收回1100份测评表,随机抽取了100份作为样本,得到如下数据:

(1)从表中数据估计,收回的测评表中,评分不小于80分的女性人数;
(2)该公司根据经验,对此APP使用者划分“用户类型”:评分不小于80分的为“A类用户”,评分小于80分的为“B类用户
(i)请根据100个样本数据,完成下面列联表:

(ⅱ)根据列联表判断能否有95%的把握认为“用户类型”与性别有关?
附:K2

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,经过点
,经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线![]() 的方程和焦点
的方程和焦点![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
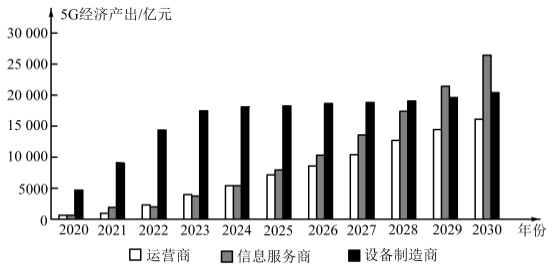
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com