
【题目】已知平行四边形ABCD的三个顶点的坐标为![]()
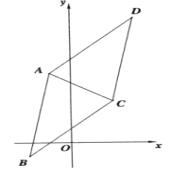
(1)求平行四边形ABCD的顶点D的坐标;
(2)求四边形ABCD的面积
(3)求![]() 的平分线所在直线方程。
的平分线所在直线方程。
科目:高中数学 来源: 题型:
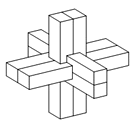
【题目】如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即樟卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四校柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱的高为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一个社区微信群“步行者”有成员100人,其中男性70人,女性30人,现统计他们平均每天步行的时间,得到频率分布直方图,如图所示:

若规定平均每天步行时间不少于2小时的成员为“步行健将”,低于2小时的成员为“非步行健将”.已知“步行健将”中女性占![]() .
.
(1)填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;

(2)现从“步行健将”中随机选派2人参加全市业余步行比赛,求2人中男性的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个数字中任取
这五个数字中任取![]() 个组成无重复数字的三位数,当三个数字中有
个组成无重复数字的三位数,当三个数字中有![]() 和
和![]() 时,
时,![]() 需排在
需排在![]() 的前面(不一定相邻),这样的三位数有( )个.
的前面(不一定相邻),这样的三位数有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是椭圆
是椭圆![]() 的焦点,
的焦点, ![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() 且与椭圆
且与椭圆![]() 相切的直线
相切的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,求证:
,求证: ![]() 的面积为定值,并求出这个定值.
的面积为定值,并求出这个定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+ , 求gn(x)的表达式;
(2)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(3)设n∈N+ , 比较g(1)+g(2)+…+g(n)与n﹣f(n)的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABC—DEF中,若AB//DE,BC//EF.
(1)求证:平面ABC//平面DEF;
(2)已知![]() 是二面角C-AD-E的平面角.求证:平面ABC
是二面角C-AD-E的平面角.求证:平面ABC![]() 平面DABE.
平面DABE.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了![]() 件产品作为样本逐件称出它们的重量(单位:克),重量值落在
件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求出甲(同组中的重量值用组中点值代替)方案样本中![]() 件产品的平均数;
件产品的平均数;
(2)若以频率作为概率,试估计从两种方案分别任取![]() 件产品,恰好两件产品都是合格品的概率分别是多少;
件产品,恰好两件产品都是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式: 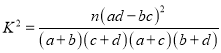 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com